Függvénylista statisztikák eszköztár
Alkotó hierarchikus fa bináris klaszterek
Z = kötés (Y)
Z = kötés (Y, 'módszer')
Z = rudazat (Y) funkció lehetővé teszi, hogy egy hierarchikus fa bináris csoportosítási algoritmus használatával. A bemeneti argumentum Y vektor közötti távolságok pár a több adatforrás tárgyak a többdimenziós térben. A száma vektor elemek egyenlő Y, ahol - az objektumok száma az eredeti adathalmaz. Y lehet beszerezni, mint kimeneti paraméter pdist funkciót. Általában, a bemeneti argumentum Y lehet meghatározni, mint egy mátrix közötti távolságok pár kezdeti számos adatobjektum szerint a formátum a kimeneti paraméter pdist funkciót.
Output paraméter Z egy mátrix, amely információkat tartalmaz a klaszter fa. Z a dimenzió. Véges klaszter-fa csomópontok a tárgyak az eredeti adathalmaz - megfigyelések többváltozós véletlen változó Y, 1-től m. Végponti csomópontot hogy elszigetelt klaszterek. Ezek fürtözött fedő facsomópontok. Minden további fedő csomópontja klaszter megfelel i-edik sorának a mátrix Z. Ő társított m index + i.
Oszlopok 1 és 2 a mátrix Z tartalmaz indexek objektumok kapcsolódik az új klaszter. A klaszterek száma képződött egyenlő bináris (m-1).
3. oszlopában a mátrix Z tartalmaz egy értéket közötti távolságok pár tárgyak kombinált klaszterekbe.
Tegyük fel, hogy a klaszterben 30 fa mag gyűjtemény. Amennyiben a 10. klasztert kombinálásával kialakított 5-én és 7-én tárgyak, és a távolság közöttük 1,5, akkor a 10. sorban a mátrix Z tartalmazza a következő értékeket Z (:, 10) = [6 május 1.5]. Ez a klaszter lesz indexe 10 + 30 = 40. Ha a 40 kódot észlelt a következő sorokban Z, ez azt jelenti, hogy a 40 bináris klaszter összevonásra kerül egy új felette klaszter.
Z = kötés (Y, „módszer”) bemeneti argumentum „módszer” lehetővé teszi, hogy adjon meg egy csoportosítási algoritmus. Egy bemeneti argumentum érték „módszer” úgy definiáljuk, mint egy teszt vonalat. A következő csoportosítási algoritmusok
ahol - r és s súlypontjai a fürtöket.
Ennek eredményeként a súlypontja algoritmus nem érhető el monoton klaszter fa. Ez akkor fordulhat elő, ha a távolság a unió két klaszter, a harmadik klaszter kisebb, mint a távolság a R vagy S k. Ebben az esetben a dendrogram megváltoztathatja az irányt, ami az oka egy másik csoportosítási algoritmus.
ahol - a távolság a klaszterek r és s, úgy határozzuk meg, egy centroid algoritmus. Inkrementális algoritmus alapján a növekedés teljes négyzetösszeg Csoporton belüli csatlakozása csoportok r és s. Csoporton belüli négyzetek összege a négyzetének összege közötti távolságok minden tárgyat a klaszter és a klaszter súlypontja.
Példák a használata a funkció kialakítására hierarchikus fa bináris klaszterek
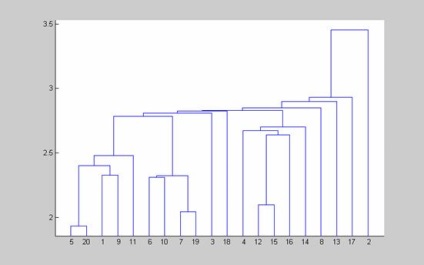
1. képződése bináris fa hierarchikus klaszter egy 10-dimenziós normális eloszlású. Az objektumok száma az egy sor bemeneti adatok 20. A grafikus ábrázolása a bináris klaszter fát alkalmazásával végezzük dendrogramot funkciót.
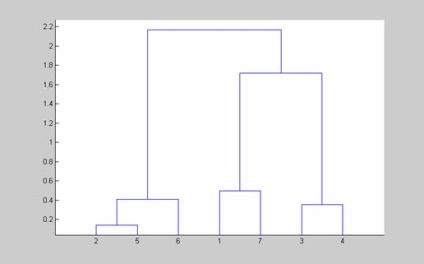
2. képződése bináris fa hierarchikus klaszter kétdimenziós véletlen változó. Az objektumok száma a beállított forrás adatok egyenlő 7. Különböző csoportosítási algoritmusok hasonlítjuk össze. Grafikus ábrázolása a csoportosításának eredményeit által végzett dendrogramot funkciót.
2.1. háttér:
2.2. Klaszterek egy algoritmus
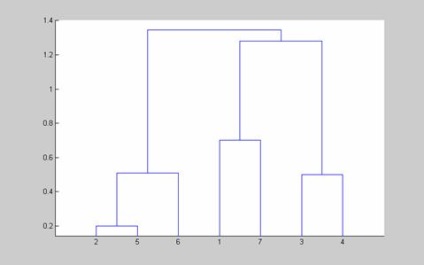
2.3. Klaszterek egy algoritmus
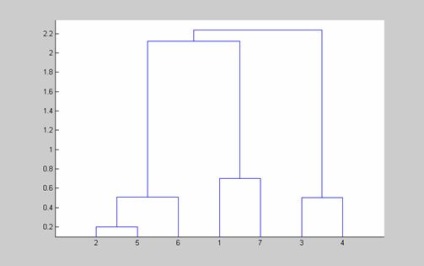
2.4. Klaszterek egy algoritmus
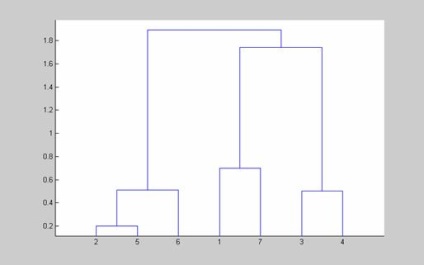
2.5. Csoportosítási algoritmus segítségével súlypontja algoritmus
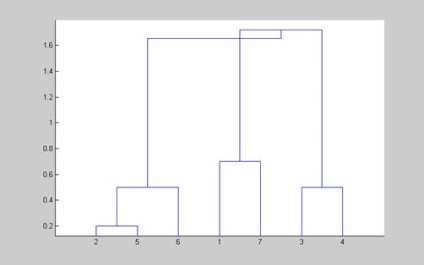
2.6. Csoportosítási algoritmus segítségével inkrementális algoritmus