Függő és független események, annak valószínűsége, hogy a termék a két esemény
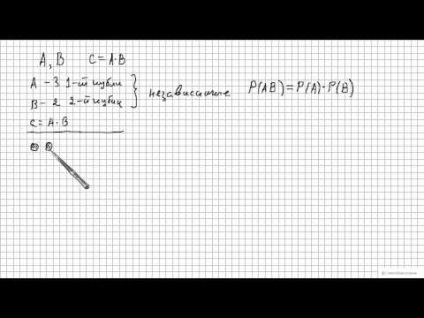
Vegyünk két véletlenszerű események és B. És mi határozza meg az eseményt, mint egy harmadik C
Ezután, C esemény lehet értelmezni, mint az egyidejű előfordulása események és az A és B események a kísérlet során. Általában az „és” az elmélet a valószínűség is lehetséges (de nagyon óvatosan) úgy kell értelmezni, mint egy matematikai szorzás. Tekintsük a példák a termék két véletlen eseményeket. Dob két kockával, és kiterjed fejlesztések:
A - elvesztése 3-1 köbméter;
B - veszteség a 2 és 2-m-kocka.
Ezután egy esemény lehet értelmezni, mint az egyidejű elvesztése 3. az első kocka, és a 2-es szám a második. Itt meg kell jegyeznünk egy fontos pont: az A és B események függetlenek egymástól, azaz a nem számít, hány esett az 1. kocka nem befolyásolja a számot, hogy esik a második, és fordítva. Az elmélet a valószínűségi események, amelyek megjelenése nem befolyásolja előfordulása más eseményeket a kísérlet során azt mondta, hogy független. És a valószínűsége független események
A második példa. Tegyük fel, van egy urna 2 fekete és 3 fehér golyó. Golyókat el egymás kiveszik a dobozból (nem kerül vissza bele). Mi megkülönböztetni a két dolgot:
A - fehér golyó eltávolítjuk;
B - elővett egy fekete golyót.
Ebben az esetben az esemény a következőképpen kell értelmezni: az első, kivette a fehér golyó, majd fekete. Kiszámítjuk a valószínűségét egy esemény C. Nyilvánvaló, hogy a kezdeti valószínűsége és B események egyenlő:
De ez a probléma is van egy ellentmondás. Mivel tartjuk a valószínűsége olyan esemény, amelyben a fehér golyó először szelektálták, majd fekete, majd a valószínűsége, hogy a második esemény (B esemény) fog változni, ha az A esemény történik, mert Az urna lesz eggyel kevesebb labdát, és a fehér golyó 2. Ezután a valószínűsége, hogy a B esemény, feltéve, hogy az esemény egy már bekövetkezett egyenlő
és az úgynevezett feltételes valószínűsége, hogy a B esemény, és az esemény az A és B - függő eseményeket. Ennek eredményeként, azt találjuk, hogy a valószínűsége, hogy egy termék két függő események
Meg kell jegyezni, hogy a valószínűsége, hogy a termék a két függő események általánosságban írhatjuk
Valóban, a mi példánkban ez nem számít, milyen sorrendben lesznek távolítva a fehér és fekete golyó, ami a legfontosabb, hogy ennek eredményeképpen kiderült, hogy az egyik golyó fehér, és a többi - fekete, ez lesz az esemény.
Így, kiszámításakor a termék a két valószínűség az események, ha azok szükségesek annak meghatározására, hogy vagy nem függ, majd az egyik a két számítási képletek.