Fresnel diffrakció egyszerű akadályok
Tekintsük diffrakciós konvergáló sugarak, vagy Fresnel diffrakció végzett abban az esetben, ha a diffrakciós mintázat figyelhető meg véges távolság az akadályok okozta diffrakciós.
Diffrakciós egy kör alakú nyílást
Pose az útját a gömb alakú hullám fény átlátszatlan képernyőt egy kerek lyuk sugara. A képernyő van elhelyezve, hogy a merőleges S egy átlátszatlan képernyőn, esik pontosan a közepén a lyuk (ábra. 9.3).
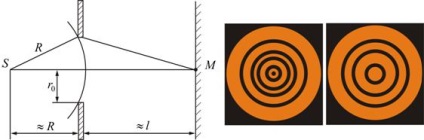
A folytatása ennek merőleges hogy egy M pont, és átgondolni, hogy mi fogjuk látni a képernyőn.
Osztjuk a nyitott része a hullám Fresnel zóna a felületen. Részletek a diffrakciós minta számától függ Fresnel zóna nyit a nyílást. A amplitúdója a kapott oszcilláció izgatott egy M pontban az összes zóna (9.2.1) és (9.2.2),
Így, amikor a furat kinyílik páratlan számú Fresnel zónák, az amplitúdó (intenzitás) át az M pont nagyobb lesz, mint a szabad terjedési hullám; Ha még. az amplitúdó (intenzitás) egyenlő nullával, ábrán látható. 9.3.
Természetesen, ha. akkor nem diffrakciós minta nem.
A diffrakciós a lemez
Gömb alakú hullám terjesztő egy pontszerű forrásból S. meghajtó megfelel az útjába (ábra. 9.4).
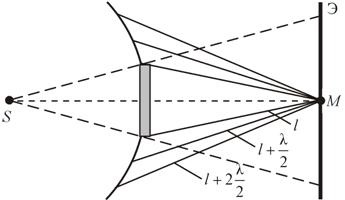

M fekszik a merőleges a lemez középpontja. Az első Fresnel zónában alapul a tárcsa pereme, és így tovább. D.
A rezgés amplitúdója fény az M pont felével egyenlő az amplitúdó miatt az első nyílt területen. Ha a lemez mérete kicsi (borító kis számú zóna), az intézkedés az első zóna kissé eltér a központi terület a hullámfront. Így a megvilágítás a ponton M azonos mivel annak hiányában a képernyő. Mivel a szimmetria a központi fénypont lesz gyűrűjében a fény és az árnyék (határain kívül a geometriai árnyék).
Paradox első pillantásra, azt a következtetést, amelynek értelmében a közepén a geometriai árnyék lehet egy fényes pontot hozta Poisson 1818-ban és később róla nevezték el. „Arago spot” megerősíti a helyességét Fresnel elmélete.
Fresnel zónák Fraunhofer diffrakciós módszerrel