Fizika (alapvető törvények és képletek)
A két hosszú egyenes vonalú és párhuzamos huzalok, amelyek közötti távolság d = 4 cm, ellentétes irányban áramlik I1 = 0,3 A, I2 = 0,5 A. megtalálni a mágneses mező indukció a pont, amely a távolság r = 2 cm-re az első és vezetékeket a sorfolytató összekötő vezetékek (8. ábra).
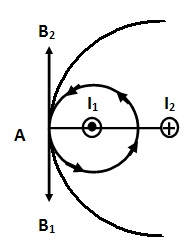
Ábra. 8 vezetékek vannak elrendezve síkjára merőleges a rajz. Kis körökben ábrázolt huzal keresztmetszete. Egyetértünk azzal, hogy az I1 áram. Úgy folyik a számunkra, és a jelenlegi I2 # 150; nbsp minket. Általános indukció B pontnál A jelentése megegyezik a vektor (geometrikus) összege a B1 indukció. és B1 területeken előállított egyenként minden aktuális t. e,
Ahhoz, hogy megtalálja az irányt a vektor B1 és B2. felhívni keresztül pont erővonalai a mágneses terek által létrehozott áramok I1 és I2.
A mágneses mező vonalak egyenes huzal hordozó egy aktuális koncentrikus körök középpontja a tengelye a huzal. Az irány az erővonal egybeesik a mozgását a nyél vége a jobb oldali csavart, csavarva az aktuális irány (jobb oldali szabály) Ezért a erővonal a mágneses mező aktuális I1. áthalad a pont, ez egy sugarú kör I1 A, és a mágneses erővonalak a jelenlegi I2. áthaladó ugyanazon a ponton, - a körön I2 A (. A 8. ábra csak egy része a kerülete). Szerint a jobbkéz-szabályt, azt találjuk, hogy a erővonal a mágneses mező I1 irányul az óramutató járásával ellentétes, és a jelenlegi I2 # 150; óramutató járásával megegyező irányban.
Most már könnyű megtalálni az irányt a vektorok B1 és B2 a ponton A: mindegyik irányul mentén érintő a megfelelő erővonal ezen a ponton. Mivel a B1 és B2 vektorok mentén irányul egy egyenesen ellenkező irányban, akkor a vektor (1) egyenlet helyettesíteni lehet egy algebrai egyenlettel
Indukciója a mágneses mező az aktuális I, átfolyik a közvetlen végtelen hosszú huzalok, a következő képlet alapján számítható
ahol # 956; 0 # 150; nbsp Mágneses állandó; # 956; # 150; nbsp propitsaemost mágneses közeg, amelyben a vezeték van; r # 150; nbsprasstoyanie a vezetéket a pont, amelynél az indukciós meghatározzuk. Behelyettesítve expressziós B1 és B2 a (2) egyenletnek, azt kapjuk,