Fénytörés lencse - studopediya
2.2.5. Az általános képlet a lencse.
gömb alakú felületek központú rendszer nevezzük, ha a központok a felületek fekvő ugyanazon a vonalon.
Az arány a gömbfelület szekvenciálisan lehet alkalmazni, hogy valamennyi felület, valamint a Lagrange-Helmholtz kapcsolat
A legegyszerűbb központú szisztematikus vékony lencse által határolt gömb alakú felületek görbületi sugara, és a
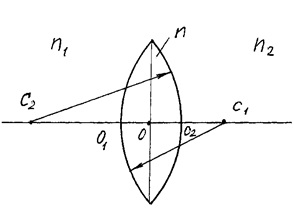
A lencsék mindkét oldalán domború, sík-domború, bikonkáv, sík-konkáv, konkáv-konvex.
Gyűjtés lencsét nevezzük, ha paraxiális párhuzamos sugarak a sugár után fénytörés találkozik egy ponton, és a szórási ha az eredmény a fénytörő lencse egy nyaláb párhuzamos sugarak alakítjuk köteg divergensek.
Egy lencse akkor tekinthető, hogy vékony, ha a vastagsága kisebb, mint a görbületi sugár és a határoló felületek. Ebben az esetben, a csúcsai a gömb alakú felületek összeolvad lényegében egyetlen pontban O. nevezett optikai középpontja a lencse.
Bármilyen átmenő optikai középpontján a lencse nevezzük az optikai tengellyel. Az optikai tengely, amely egybeesik a szimmetriatengelye a rendszer, az úgynevezett elsődleges, és a fennmaradó oldal.
Bármilyen paraxialis ray áthaladó optikai középpontja a lencse nem tapasztal fénytörés.
Vegyünk egy pontforrás kép által létrehozott vékony lencse görbületi sugara.
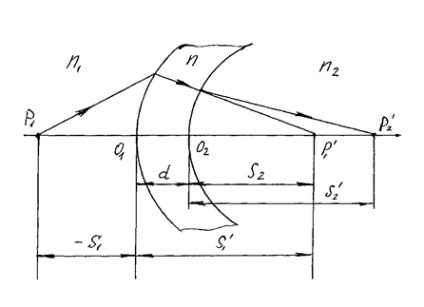
Írunk a képlet gömb alakú felületekre
Amennyiben - d; n-Törésmutató lencse, és a törésmutató a média előtt és után a lencse.
Egy vékony lencse. Kombinálása (1) és (2) kapjunk egy vékony lencse képletű
Ha a lencse található, egy homogén környezetben,
Kapunk egy általános képletű formájában egy vékony lencse:
Jelölő - relatív refrakciós index a lencse anyaga tekintetében a közepes, megkapjuk
2.2.6. Optikai teljesítmény és a fókusztávolság a lencse.
Az egyenlet formájában egy vékony lencse:
Ahol F optikai teljesítménye egy vékony lencse. Ez összegével egyenlő optikai jogkörrel, gömb alakú felületekre. Mivel a (6) egyenlet teljesül minden paraxialis sugarai a fény, az homocentric sugár után fénytörés marad homocentric és stigmatizált kép.
Egy lencse, található egy homogén közegben a törésmutató, az optikai teljesítmény határozza meg a képlet:
Egy vékony lencse bevezetni a fogalmak első és hátsó súlypontja és gyújtótávolság és.
A hátsó gyújtótávolság (8)
Az első fókusztávolság (9)
Így: (10)
Ha a közeget, amelyben a lencse van elhelyezve, a levegő, m = 1, és az optikai teljesítmény a lencse mögött az a fókusztávolság arány:
Ha mindkét oldalán a különböző környezetekben a lencse, akkor a kapcsolat:
2.2.7. Newton formula. A növekedés a lencse.
Vékony lencse egyenlet továbbra is használható, mint a Newton képletű
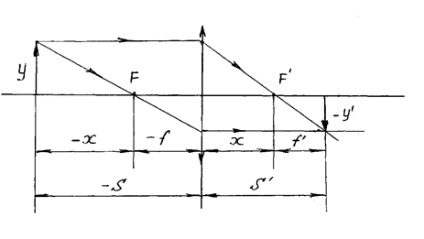
és ahol - a távolság a tárgy és a kép, mérve a fő gócok.
A növekedés a lencsék által meghatározott képletek.
2.2.8. Épület képet a lencséket.
A konstrukció által alkotott kép egy vékony lencse, kényelmes a használata a következő szabályok eredő alapvető meghatározások és az eredményeket (3.).
1.Luch áthaladó optikai középpontja a lencse található, egy homogén környezetben, nem törik.
2.Luch párhuzamosak a fő optikai tengely után fénytörés áthalad a hátsó fő fókusz, ha a lencse összegyűjti, és folytatódjon a sugár keresztezi a fő fókusz, egyik oldalán helyezkedik el a témát, ha a lencse eltérő.
3.Luch a lencsén áthaladó fő hangsúly után fénytörés párhuzamos a fő optikai tengelyre.
4.Luch párhuzamos oldala az optikai tengely után fénytörés áthalad a hátsó oldalán fókuszpontja a lencse, ha a lencse összegyűjti, és átmegy a folytatása az első oldalon fókuszt, ha a diffúziós lencse.
segédfény konstrukció az építőiparban során bármely ray után fénytörés egy vékony lencse, ezzel párhuzamosan, és áthalad az optikai központ. A metszéspontja a kiegészítő gerenda a fókuszsík meghatározza az oldalsó hangsúly, amelyben az összes lehetséges keresztgerendák, ezzel párhuzamosan.
1. Szerezzen egy vékony lencse képlet.
2. Milyen az optikai teljesítmény a vékony lencse?
3. Hogyan gyújtótávolságú objektívek vékony?
4. Lehet lentikuláris lencse kell gyűjteni?
önálló munka feladat.
Tekintsük self-képalkotó vékony lencsék különböző pozíciókban az objektum.
1. DV sivukhin Az általános tanfolyam fizika Optika: Proc. Juttatás. - M. Science, 1985-725s.
2. Landsberg GS optika. - M. Science 1976.
3. Savelyev IV Természetesen az általános fizika. T.2.M. Tudomány, 1988-478s.; V.3 1988-205s.
4. Boutique EI Optika.-M. Vyssh.shkola, 1986-512S.
5. Kalitievsky NI Hullám optika. - M. Vyssh.shkola, 1978,383s.
2.3.Tsentrirovannaya optikai rendszer.
2.3.1 Az elmélet Gauss az ideális optikai rendszert.
Bármilyen optikai rendszer gyűjteménye központú megtörő és visszaverő felületek. Egy ideális optikai rendszer tárolt homocentricity gerendák és egy kép geometriailag hasonló a tárgya, azaz, Minden pont, vonal, sík a objektumtérben mérkőzés pont, vonal, sík a képen térben. Az elmélet tökéletesen központosítva optikai rendszerek által kifejlesztett Gauss 1841-ben. és ez egy speciális esete az általánosabb probléma geometriai transzformáció egy helyet egy másik, amely az úgynevezett kollineáris átalakulás. Gauss elmélet meghatároz számos úgynevezett sarkalatos pontok és síkok, melynek feladata a teljes tulajdonságait ismerteti, az optikai rendszer, és lehetővé teszi, hogy használja, tekintet nélkül a tényleges során sugarak a rendszerben.
Tekintsük a fénytörés egy gömb alakú felületen.
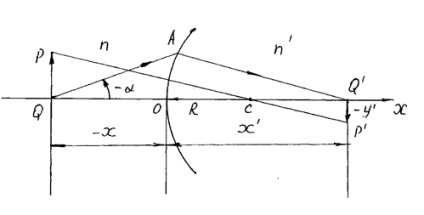
Tól (1) és (2) úgy kapjuk átalakításával képletű
(3) képlet tudunk az alapján geometriai elmélet bármely központú rendszerek paraxialis sugarak homocentric. Ezzel az egymást követő alkalmazás kaphat helyet az utolsó kép által az egész rendszert. Ezek a képletek meghatározott egyenesre közötti levelezés pontok objektumterületet és a kép térben pontokat.
Tól kollineáris megfelelő képletek következő tulajdonságokat optikai képek központú rendszerek.
1. Minden sík objektumterület van ábrázolva, mint egy sík
2. Minden sor ábrázolják, mint egy egyenes vonal a térben tárgyak
3. Minden pont a objektumterület képviseli, mint egy pont a térben
2.3.2 bíboros sík és pont.
A lényeg a gépet, és egy optikai rendszert.
Két konjugált síkok, amelyek látszólag egymással növelik a határokon
. Ezek az úgynevezett fősíkjaikkal és
A metszéspontjai fősíkjaikkal a fő optikai tengely, az úgynevezett fő pontokat.
A helyzet a fő síkok által meghatározott görbületi sugarak a fénytörő és a fényvisszaverő felületek, a köztük lévő távolságot, és a törésmutatója a média által körülhatárolt ezeket a felületeket. Ezért, a fő síkok lehetnek belül és kívül egyaránt a rendszer, mind ugyanazon oldalán határoló felületei a rendszer, és a mindkét oldalon.
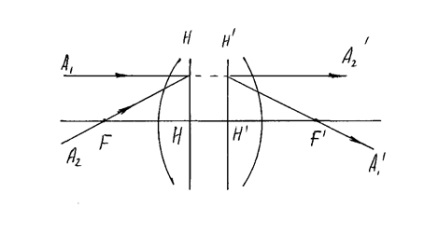
H -Front elsődleges sík, -az hátsó fősíkjánál
Fókuszsíkon és a fókusz az optikai rendszer.
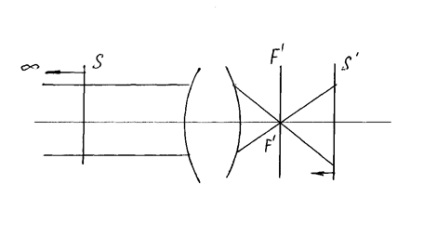
A hátsó fókuszsíkjában a sík konjugált végtelenhez található egy sík térbeli tárgyak. tengelyére merőleges. A metszéspont a hátsó fókuszsíkjában fő optikai tengelyen a helyzet a hátsó fókusz rendszer (F) (3.).
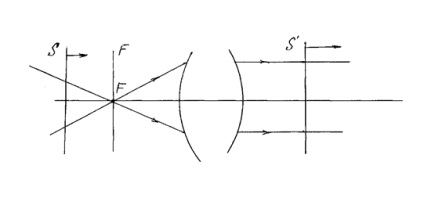
Első képérzékelő síkja sík konjugált a végtelenben található a tér sík képeket. tengelyére merőleges. A metszéspontja az elülső fókuszsíkjában fő optikai tengelyen a helyzetben az első hangsúly a rendszer (F) (ábra. 4).
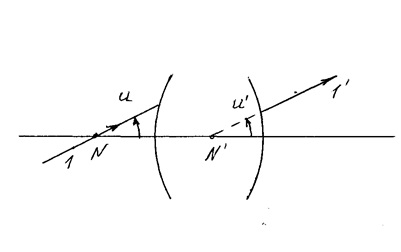
Csomópont és sík
Nevű csomóponton feküdt az optikai tengelyen konjugátum pontok N, és rendelkeznek azzal a tulajdonsággal, hogy áthaladnak őket (vagy valójában belül a képzeletbeli meghosszabbítása a rendszer) a konjugátum gerendák párhuzamosak egymással (azaz, a szögletes nagyítás arány)
Merőleges síkban a tengelyre, és áthalad a csomóponti síkjában nevezzük csomópontok. Ha a média mindkét oldalán a rendszer ugyanaz, akkor a csomópontok egybeesik a fő.
2.3.3. A képlet az optikai rendszer.
A konstrukció a képet középre az ideális rendszer, akkor a következő szabályokat:
1) A nyaláb fókuszán átmenő F, kilép a rendszer párhuzamosan az optikai tengelyt a pontban megadott úgy, hogy a folytatása a bejövő és kimenő gerendák pontban metszik egymást tartozó fősík H;
2) A sugár esemény párhuzamos az optikai tengellyel, a kilépő ponton fut úgy, hogy a továbbiakban a bejövő és kimenő gerendák pontban metszik egymást tartozó hátsó fő síkja.
3) nyaláb beeső úgy, hogy annak kiterjesztését metszi a rögzítési pontban N. kijelentkezésekor párhuzamos a bejövő, és annak meghosszabbítását metszi az optikai tengely a csomóponthoz.
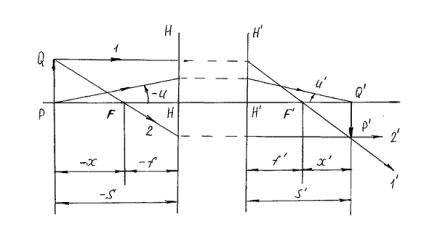
Alapvető kapcsolatok jellemzésére központú ideális optikai rendszer, a következő
Newton képletű (4)
A képlet a (5)
A gyújtótávolság mérjük a fő síkok.
Az optikai teljesítménye a rendszer határozza meg a képlet:
Ha az F> 0, a rendszer az úgynevezett gyűjtése, F<0 – рассеивающей
A gyújtótávolság kapcsolódnak által származtatására kapcsolatban Lagrange-Helmholtz
2.3.4 Fokozott rendszer.
A növekedés központú rendszer alkalmazásával állíthatjuk elő a Lagrange-Helmholtz formula. és képletek származó geometriai viszonyok (6. ábra)