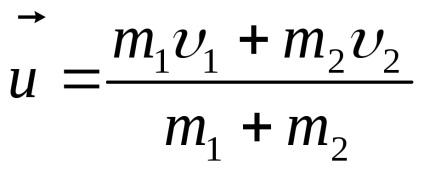F 1 Mechanikus dinamikáját elhelyezhet 2
Mechanikus Dynamics 1 2 transzlációs mozgást
AksiomaI. A törvény a tehetetlenség: Anyagi tárolja a nyugalmi állapotban, illetve egységes egyenes vonalú mozgás, amíg amíg valamilyen erő nem fogja megváltoztatni ezt az állapotot.
AksiomaII. Az alaptörvény a mechanika a tehetetlenségi koordinátarendszerben ható erő a részecske, gyorsulását okozza arányos ez az erő és az az irány vonal mentén a keresete



A

AksiomaIV. A szuperpozíció elve: A gyorsulás az anyagi pont alatt egyidejű hatása több erő rá ugyanaz a vektor összege gyorsulások közölt vele magánlakás, ahol

egyetemes tömegvonzás törvénye: két lényeges ponton vonzódnak egymáshoz erő arányos a tömeg az anyag pont és fordítottan arányos a távolság négyzetével közöttük




A súrlódási erő:


A lendület a lényeges pont

A tétel változásának lendület a anyagi pont differenciális formában: az első alkalommal származéka a lendület egy anyagi pont megegyezik az összeg az összes ható erők egy anyagi pont

Tétel változási lendület anyagi pont az integrált formában:

A törvény lendületmegmaradás egy anyagi pont: ha a kapott az erőtől, amely az anyagi pont nullával egyenlő, a lendület anyagi pont állandó marad



A sugár vektor a tömegközéppont:
Rendszer pont

az anyagi test

Egy rendszer testek

a tömegközéppontja koordináták:
A pontrendszer;
az anyagi test;
Egy rendszer anyagi testek.
A sebesség és a gyorsulás a tömegközéppont:


Rendszer pont


az anyagi test


Egy rendszer testek
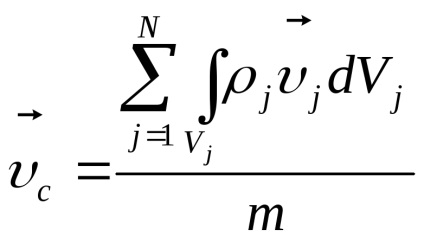

A kiemelkedések a sebesség és a gyorsulás a tömegközéppont:;

A pontrendszer;
;
az anyagi test;
;
egy rendszer testecskék;
.
Tétel a mozgás a tömegközéppontja a mechanikai rendszer: a fő vektor a külső erők egyenlő a termék tömegének a mechanikai rendszer a gyorsulás a tömegközéppontja.
Tétel változási lendület a mechanikai rendszert differenciális formában: először származéka a lendület a mechanikai rendszer az elsődleges vektora a külső erők


Rendszer pont


az anyagi test


Egy rendszer testek


A törvény lendületmegmaradás mechanikai rendszer: ha egy mechanikus rendszer zárt (


A törvény lendületmegmaradás esetén egy tökéletesen rugalmas ütközés két szervek:, ahol

Ha rugalmatlan ütközés, amikor az ütközés test összeragadnak után teljes sebességgel