Építése a mag rész
Ha a pont alkalmazásának F erő található a határszakaszon a kernel, a nyúlási szakasz lesz. Végtelenül áramtalanítja a mag vezet, mi lesz a zónával, azt jelentette, hogy a pont határ mag nullavezetŒvel mi oldalunkon.
Ezért építeni a kernel meg kell vizsgálni, mindenféle érintők, hogy a szakasz és megtalálni ezekben az esetekben a lényeg az erő alkalmazását. Majd ezeket összekötő pontokat, azt látjuk, részben a mag.
Ha a kontúr áll egyenes szakaszokból alapfeladata épület sokkal könnyebb.
Tekintsük a kernel építmények eljárás részben.
Az egyenlet I-edik semleges vonal (ris.19.15). Ez az egyenlet áthalad a két pontot 1-2:
Egyenlet (19,9) meg kell egyeznie a egyenlet (19,8). Így, egyenlet (19,9) ismert, és ismert. Meg kell találni.
Ehhez először tegyük az x = 0. A kapcsolatok (19,9), azt látjuk, y. pótlásának x, y egyenlet (19,8), és megtalálni uF.
A megállapítás arra utalnak, XF y = 0. általános képlet (19,9) találj x, behelyettesítjük ezeket a x és y egyenletben (19,8), és megtalálja XF.
Fontos megjegyzés. Vegyünk egy sarokpont B. B pont után töltheti végtelen számú érintőleges.
Azonban, minden vonal ponton áthaladó B. által leírt egyenlettel, amely kielégíti helyettesítésével. Helyettesíti azokat az egyenlet (19,8):
Mert. - egy jól ismert számot, az eredmény egy
ahol a, b, c - állandók. Ez az egyenes egyenlete. amelyen a pontok a nukleáris határt.
Így, amikor megy egyik oldalról a másikra BC BD. Nem kell keresni, és akkor csak meg kell kapcsolódni két pontot egy egyenes határ a sejtmag, amelyeket kapott a BC és BD.
Tekintsük a példát. Találunk részben a lényege a téglalap.
Az i-edik nullavezetŒvel egyenlet (19,9) a formája:
Ezután (19,8) formáját ölti:
Megszorozzuk kapjuk:
Hisszük első x = 0, akkor a (19.10) az következik, hogy. Behelyettesítve a (19.11), kapjuk:
Találunk az XF. Mivel (19.10) is feltételezi, hogy csak. Ezután elindultunk. x - tetszőleges számú, például X = b / 2. Behelyettesítve a (19,11), azt találjuk:
Hasonlóképpen találunk egy pont keresztmetszeti határa a mag az esetben, ha a semleges vonal húzódik függőlegesen (II-edik semleges vonal), majd megkapjuk. .
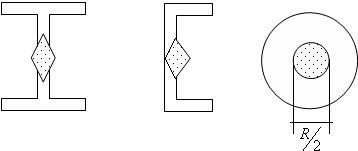
Hasonlóképpen, egy másik 2 pontot meghatározva. Az eredmény egy olyan keresztmetszete a mag ábrán bemutatott (19.16) formájában egy rombusz.
Egy I-gerenda, csatornák, tartomány részben atommag típusok látható (ris.19.17).
Bizonyos esetekben az épület építési ütközési erők, amelyek a gyorsan változó idővel. Ez ahhoz vezethet, hogy két veszélyes következményei:
1) A dinamikus hatásokat meghaladhatja a statikus hatás a külső erők és időben akár több száz alkalommal.
2) Lehet, hogy egy jelenség a rezonancia.
2 módja van a probléma megoldásának meghatározása dinamikus hatásokat szerkezetét szervek. Ezek alapján rendre a következő két törvény: a törvény az energiamegmaradás elvét és a D'Alembert.
Tekintsük a probléma az esés a rakomány tömege F = mg amelynek a H magassága (sm.ris.20.1).
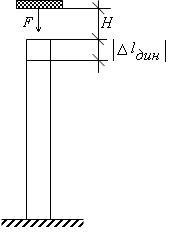
Tervező érdekelt a maximális erő hatása, amit úgy hívunk erő hatására. Együtt ez a probléma, úgy a fiktív probléma, amikor az erő a rúd. amely egyenlő a testtömege F.
Force jelöljük sztrájk. Egyértelmű, hogy :.
Bemutatjuk dinamikus tényező:
Ezután a dinamikus feszültség lesz
Szerint (1,20), kapjuk:
Így a probléma csökkenti a számítás a számot. Meghatározni, hogy használja a törvény az energiamegmaradás.
Falling Georgia elkövetett valami munkát. Ez a munka nem tűnik el, az átalakul energiát sűrített rúd deformáció.
Jelöljük: - A munkaerő F; - az energia deformáció a rúd. majd
Először kiszámítjuk W:
Itt - egy utat, amely figyelembe kényszeríteni F. tól ris.20.1 egyértelmű, hogy:
Kiszámoltuk az energia deformáció a rúd:
Behelyettesítve a törvény az energiamegmaradás (20,4), ezt kapjuk:
Csökkentése, így egy másodfokú egyenlet:
A megoldás a következő formában:
Ez az alapvető képlet a dinamikus tényező. Ahol H - magassága csepp hajózás;
- dummy rúd alakváltozás probléma statikus terhelés mellett (ris.20.2)
1) Még ha az esési magasság H = 0, szerint (20,5) hirtelen terhelő erő megduplázza a súlya a rakományt.
2) A nagyobb (azaz, több csapadék rúd), annál kisebb a káros hatások a hatása, mivel kisebb lesz. Tól Hooke-törvény, az következik, hogy ezt el lehet érni a 3 módja van:
1. Növeli a hossza a rúd
2. Csökkent rúd vastagsága
3. Csökkent merevség (E) a rúd
Megjegyzés: a képlet (20,5) lehet alkalmazni a hatása a gerenda (ris.20.3). Ebben az esetben meg kell érteni a lehajlás (sm.ris.20.3):