Elsőrendű differenciálegyenlet - studopediya
Ha az egyenlet () tartalmazza csak az első származékot a kívánt funkció, ez az elsőrendű differenciálegyenlet. A leggyakoribb elsőrendű differenciálegyenlet formájában
Amennyiben egy adott folytonos függvénye három érvek: különösen, hogy nem függhet X vagy Y, de meg kell szükségszerűen tartalmaznak.
Ha az egyenlet (7,6) határozza meg, mint egy implicit függvény a másik két érv, leírható formájában megoldott tekintetében
Van egy folytonos függvény által meghatározott x és y.
A differenciálegyenlet (7,16) vagy (7,17) x a független változó a kívánt funkciót.
Opredelenie7.4 elsőrendű differenciálegyenlet egy reláció, amely kapcsolódik a kívánt funkciót, a független változók és az első származékot a kívánt funkció.
DEFINÍCIÓ 7. 5 határozata elsőrendű differenciálegyenlet semmilyen funkciót. amely és helyette egyenletben (7,16) vagy (7,17) kapcsolja be a személyazonosságát.
A differenciálegyenlet (7,17) a következő tétel, az úgynevezett a tétel a létezését.
Tétel 7.1 Az egyenletben (7,17) folytonos és annak parciális derivált folyamatos egy régiót, amely egy pontot. van egy egyedülálló megoldása az egyenletnek
,
A geometriai jelentése tétel zaklyuaetsya, hogy van egy és csak egy funkció. grafikon, amely átmegy a ponton.
Példa 7.7: Tekintsük a probléma
Amennyiben egy folytonos függvény, és a domain ennek a funkciónak a készlet minden.
Könnyen látható, hogy. azaz a feltétele a tétel. A megoldás ennek az egyenletnek
Meghatározni a feltétellel, hogy. azaz. ahol C = 1/2.
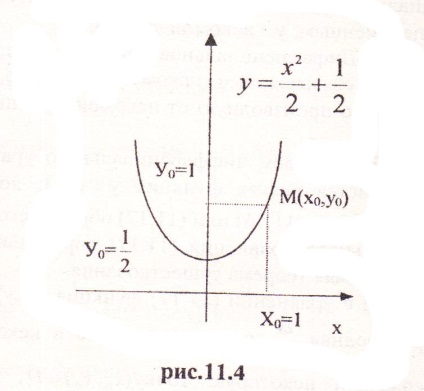
Állapotban. hogy ha x = x0 a függvény y egyenlőnek kell lennie a kezdeti előre beállított szám y0. Ez az úgynevezett kezdeti feltétel. Gyakran írott formában
Meghatározás 7.6 Az általános megoldás az elsőrendű differenciálegyenlet függvénye. amely változik egy tetszőleges C konstans, és teljesíti a következő feltételeket:
A) kielégíti a differenciálegyenlet bármely adott konstans értékét C C
B) függetlenül a kezdeti feltétel, ha meg lehet találni a értéke C = C0, amely megfelel az adott kezdeti feltétel.
Ezek minden feltétel teljesül, akkor és csak akkor, ha a feltétel a tétel a létezés és az egyediség.
A folyamat találni egy általános megoldást a differenciálegyenlet, gyakran jön a kapcsolat a forma
Nem engedélyezett képest y. lehetővé téve az arány Y tekintetében, megkapjuk az általános megoldás.
Azonban kifejezni y tekintve az arány (7,19) nem mindig lehet az elemi függvények. Ebben az esetben, az általános megoldás a differenciálegyenlet implicit.
. hallgatólagosan meghatározza a teljes megoldás, az úgynevezett közös integrál differenciálegyenlet.
Definíció 7.7: Egy különösen oldat bármely funkció. ha ez utóbbi tetszőleges konstans C hőmérsékleten, így egy bizonyos értéket C = C0.
arány az úgynevezett különleges integrál egyenlet.