elméleti mechanika
A rudak 3, 7, 11 - nevezzük függőleges. Terminal 1, 4, 9, 12 - nevezzük fogszabályozó.
Rudak, amely egy zárt háromszög, az úgynevezett farm panel.
Farm látható. 56 hat panelek.
Számításakor a gazdaságban, hogy a következő feltételezéseket.
1. Minden rudak traktor egyenes és súlytalan.
2. Egységek farm - ideális zsanérok.
3. Külső erők hatnak a csomópontok a gazdaság.
4. A rudak mezőgazdasági érzékelik kizárólag hosszanti irányú erők: nyomó vagy húzó.
farm számítás, hogy meghatározza a támogatási reakciók és a belső erők rudak gazdaságban.
Kiszámításakor támogatást reakciók mezőgazdasági tekintik szilárd test, amely hat a lapos rendszer erők. A számítás elkészítésére tervezési rendszer előkészítése az egyensúlyi egyenletek és a meghatározást az ismeretlen reakciókat.
Erők a rudak gazdaságban meghatározni:
1. Az eljárás vágó egység.
2. Módszer szakaszok (Ritter-módszer).
Összeállításakor a tervezési rendszereket úgy kell venni, hogy ha a rúd meghosszabbítják azt az erőt, amely úgy működik, a csomópontra, és utasította a csomóponttól a terminálra. Ha a rúd összenyomódik, az erő arra irányul, hogy a csomópont a rúd (ábra. 57).
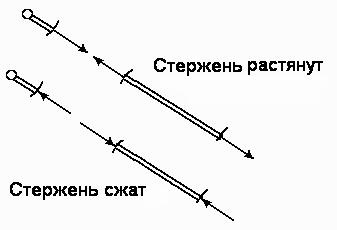
csomópont kivágási módszer alkalmazásával
node kimetszés eljárás egymást követő vágás Mezőgazdasági területek és felülvizsgálja az egyensúlyát. Mivel a csomópont jár konvergáló lapos rendszert erők, amelyek lehetséges, hogy rögzítse csak két egyensúlyi egyenletek, a csomópontok kell vágni úgy, hogy egy ismeretlen erő nem volt több, mint kettő. feltételezzük, hogy dolgozzon ki egy olyan rendszert, amely tervezési nyújtva a rudak, azaz minden belső erőfeszítéseket a jogot a csomópont a terminálra. Minden egyes csomópont áll az egyensúlyi egyenlettel
Ha az erők a rudak találhatók ezek a képletek vannak a „+” jel, akkor technikailag ez azt jelzi, hogy a rúd megnyúlik, ha a jel erőfeszítést „-”, majd a rudat összenyomódik.
A módszer a szakaszok (Ritter-módszer), hogy a gazdaságban a két részre vágtuk. Az egyik része a gazdaság visszaesett, és akció jelenik meg az erőfeszítéseket a többi rudakat, amelyek fogott a keresztmetszete. Erők a rudak mentén vannak vezetve

rudak a leesett része a kabát, hogy Ismét azt feltételezzük, hogy az összes vonal meghosszabbítását. Részének tekintendők a gazdaságban, amelyek aktívak (előre meghatározott) erőt, és az alátámasztó reakció erők a rudak egyensúlyban van. Ez pedig egy tetszőleges sík (nem konvergens) villamosenergia-rendszer, amelyhez írhatunk három egyensúlyi egyenletek. Ezért az ismeretlen erők a szakaszban nem lehet több, mint három.
Mint tudod, három formája van az egyensúlyi egyenletek egy sima rendszer:
Összeállításakor a egyenleteket van kiválasztva, a forma, amely lehetővé teszi, hogy a legtöbbet egyszerű egyenlet. Például, ha a keresztmetszeti két ismeretlen erők párhuzamosak, célszerű alkalmazni a 2. forma az egyenletek. Ha minden hatalom szakaszban különálló, harmadik formában. Ebben az esetben erők metszéspont választották a nyomaték pont. Az így kapott minden egyensúlyi egyenlet tartalmaz egy ismeretlen. Összehasonlítva a módszer vágó egység jelentősen felgyorsítja kiszámítása és növeli a pontosságot a számításokat.
Ha a szakasz több mint három ismeretlen erő, van, hogy végezzen további részén.
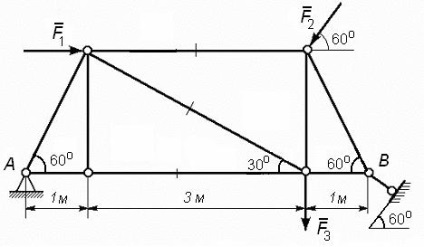
Egy példa a probléma megoldásának
A gazdaságban, ábrán látható módon. 58, vannak olyan erők F 1 = 1 kN, F 2 = F 2 kN és 3 kN = 3.
Annak meghatározására reakció támogatja erők a rudak vágással farm oldalakon. Annak ellenőrzésére, rudak jelölt erőfeszítéseinek szakaszok.
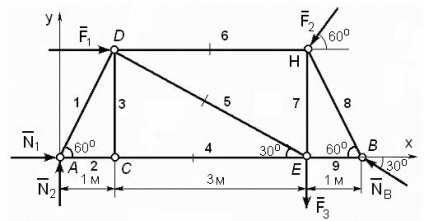
Minden betű jelöli egységek és rudak számok. Elveti az összes támogatja és cserélje ki őket támogató reakciót N 1. N 2 és N B.
Megmutatjuk koordinátatengelyeken. Az így kapott számítási rendszer ábrán látható. 59.
Nézzük a gazdaságban statikailag határozott. Farm 6 csomópontok és 9 rudak, azaz Y = 6, C = 9. Behelyettesítve ezeket az értékeket az általános képletű C = 2Y - 3, 9 kap a azonosság = 2 • 6 - 3 = 9. Farm statikailag határozott.
Annak megállapításához, a támogatási reakciók vehetik az első formája az egyensúlyi egyenletek egy sík rendszer erők.
Σ F kx = N 1 + F 1 - F 2 cos60 0 - N B cos30 = 0 0;
Σ F ky = N 2 - F 2 sin60 O - F 3 - N B sin30 o = 0;
Σ M Egy (F k) = - F TG 60 1 1 o + F 1 2 cos60 o tg 60 o - F 2 sin60 O 4 - - F 4 Március - N B sin30 o 5 = 0.
N 1 = - F 1 + F 2 cos60 O + N B cos30 o = -1+ 2 0,5 + 7,571 = 0,866 = -1 + 1 + 6,557 = 6,557kN.
N 2 = + F 2 sin60 o + F 3 - N B sin30 o = 2 + 3 0,866-7,571 0,5 = = 1,732 + 3-3,785 = 0,947 kN.
Így, N 1 = 6, 557 kN, N 2 = 0,947 kN, N B = 7,571 kN.
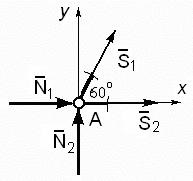
Most határozzuk meg az erők a rudak vágással farm csomópontokat. Gyökérvágógépek szerelvény lehet A vagy B csomópont, mivel azok nem ismertek erőfeszítést csak két terminál. Kezdjük a csomópont A. Vágja ki a csomópont és megvizsgálja az egyensúlyát. A csomópont aktusok konvergáló rendszer erők: reakció pólusok N 1 és N 2, és erő a rúd 1 - S 1 és a 2 rúd - S 2. törekvések célja rudak a csomópont felé a megfelelő rudak, azaz feltételezzük, hogy ezek a rudak vannak nyújtva. A pontnál helye az eredete a derékszögű koordináta-rendszert axy. Számítási terve csomópont ábrán látható. 60.
Ebben az esetben az egyensúlyi egyenletek
Σ F kx = N 1 + S 1 + S cos60 körülbelül 2 = 0;
Σ F ky = N 2 + S 1 sin60 = 0.
A második egyenletben

S 1 = - sin N 2 60 O = - 0947 0866 = -1093 kN.
Az első egyenlet találunk
S 2 = - N 1 - S 1 cos60 O = -6557 - (- 1,093) 0,5 = -6,01 kN.
A „-” jel azt mutatja, hogy mind formailag rudak tömörítik.
Mivel az erő a 2 rúd találtuk, hogy lehetséges, hogy lépni a csomóponthoz C. Ebben az esetben, az ismeretlen erők a rudak 3, 4 - S 3. S 4.
Vágja ki, és alkotják a C csomópont számítási sémát rá is, ahogy azt tette az A csomópont (ábra. 61).
egyensúlyi egyenletek
Σ F kx = - S 2 „+ S 4 = 0,
Mivel az S 2 \ = S 2 = -6,01kN. akkor az egyenletek találunk
S 4 = S 2 „= -6,01 kN. S 3 = 0.
Következésképpen, a 4 rúd van nyomva, a 3 rúd erőfeszítéseket ott. Kivágott egy áramköri csomópont D. számított ez ábrán látható. 62.
A ismeretlenek itt erők a rudak 5 és 6 - S 5. S 6.
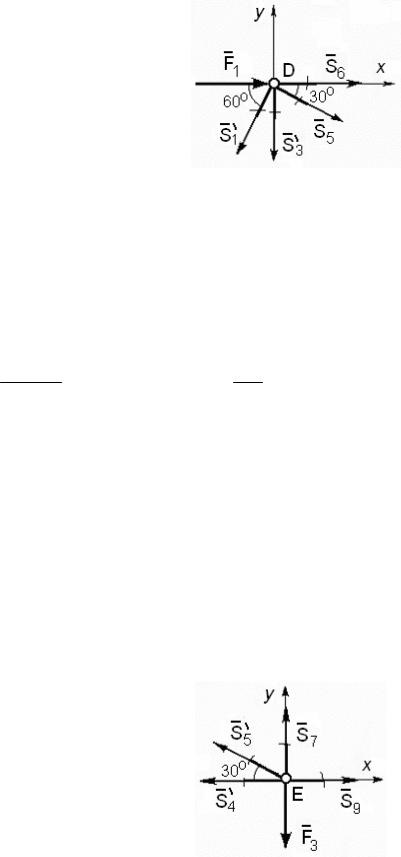
egyensúlyi egyenletek
Σ F kx = F 1 - S 1 „cos60 0 cos30 + S 5 + S 6 0 = 0,
Σ F ky = - S 1 'sin60 0 - S 3' - S 5 0 sin30 = 0.
Mivel az S 1 \ = S 1 = -1,093kN. S 3 \ = S 3 = 0, akkor azt látjuk, az egyenletekből
S 5 = sin30 1 0 (- S 1 'sin60 0 - S 3') = 0,5 1 - (-1,093) 0,866-0 = 1,893 kN. S 6 = - F 1 + S 1 „cos60 0 - S 0 = 5 cos30
= -1 + (- 1,093) 0,5 -1,893 0,866 = -3,186 kN.
A rudat 5 meghosszabbodik, a 6 rúd van tömörítve.
Mivel az erők a rudak 4, 5 és 6 talált, akkor folytassa
Kivágott áramköri csomópont E. A számított ez ábrán látható. 63. A ismeretlenek itt erők a rudak a 7. és 9. - S 7. S 9.
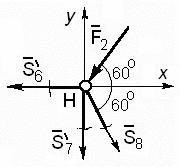
egyensúlyi egyenletek
Σ F kx = - S 4 '- S 5' cos30 + S 0 9 = 0,
Σ F ky = S 5 „sin30 0 + S 7 - F 3 = 0.
Mivel az S '4 = S 4 = -6,01 kN és S' 5 = S 5 = 1893 kN. akkor az egyenletek találunk
9 S 4 = S '+ S 5' cos30 0 = 6,01 + 1,893 0,866 = -4,371 kN. 7 = F S 3 - S 5 „sin30 0 = 3 -1,893 0,5 = 2.054 kN.
A 7 ütköző van hosszabbítva, és a 9 rúd összenyomódik.
Kivágott H. csomópont számítási sémát azt mutatja ris.64. Ismeretlen itt az erő a rúd 8 - S 8.
Az egyensúlyi egyenlet a helyszínen vannak az űrlap
Σ F kx = - S 6 „- F 2 cos60 0 + S 8 0 cos60 = 0,
Σ F ky = - S 7 „- S 8 sin60 0 - F 2 0 sin60 = 0.
Mivel az S „6 = S 6 = -3,186 kN. akkor az első egyenlet találunk
S 7 „= - S 8 sin60 0 - F 2 sin60 = 0 - (- 4,372) 0,866-0,866 2 = 2.054 kN.
Erőfeszítéseket a rúd 7, eredményezi vágásához csomópontok E és H, vonalban vannak.
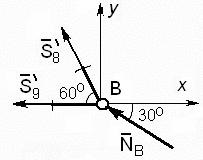
Node B lehet használni, hogy teszteljék a teljesítménye számításokat. Vágja ki a B csomópont és megvizsgálja annak egyensúlyát. Erők a 8 és 9 rudak fogják tekinteni ismeretlen. Az egyensúlyi egyenletei a B csomópont meghatározza ezeket az erőfeszítéseket. Ha egybeesik a kapcsolódó erőfeszítések fölött található, a számítás helyes - ha nem, meg kell keresni a hibát a korábbi számításokat. Számítási terve csomópont B ábrán mutatjuk be. 65.
egyensúlyi egyenlet B csomópont van formájában
Σ F kx = - S 9 '- S 8' cos60 0 - N B cos30 0 = 0,
Σ F ky = S 8 „sin60 0 + N B sin30 0 = 0.
Megoldásában egyenletrendszer találunk