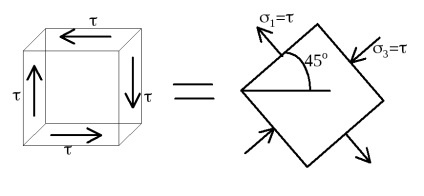
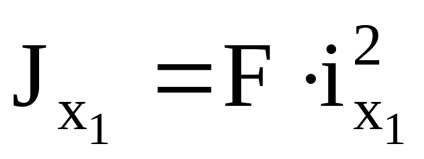egyszerű nyírás
B
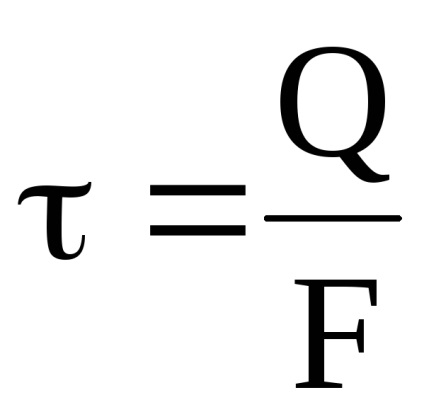
P
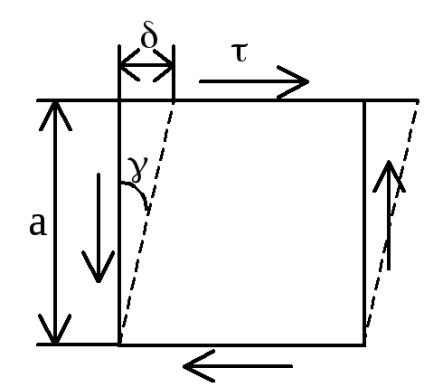

Hooke-törvény nyírási. = / G vagy = G.
G - nyírási modulus, vagy nyírási modulus [MPa] - az anyag állandó jellemző a képességét, hogy ellenálljon a deformációnak nyírási.
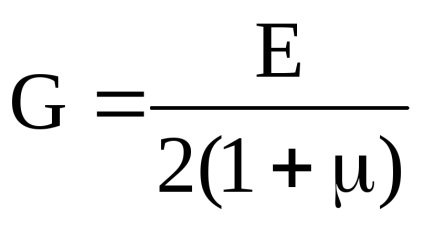
A potenciális energia nyírási:
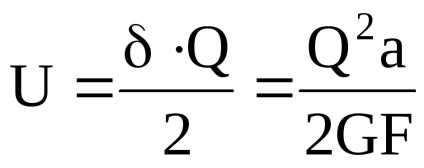
A fajlagos alakváltozási energia a nyírási:
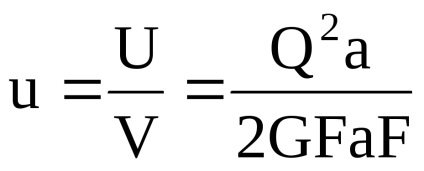
ahol V = aF - térfogata elem. Tekintettel a Hooke-törvény,
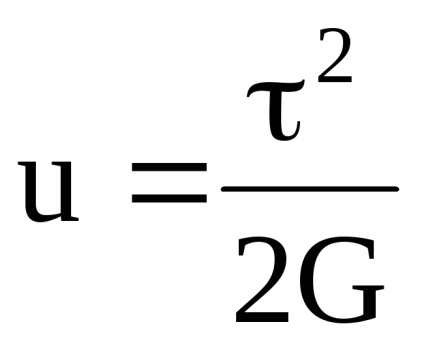
Az összes potenciális energia tiszta nyírás csak a változás alakját, a változás volumene alapján nyírási deformáció nulla.
K
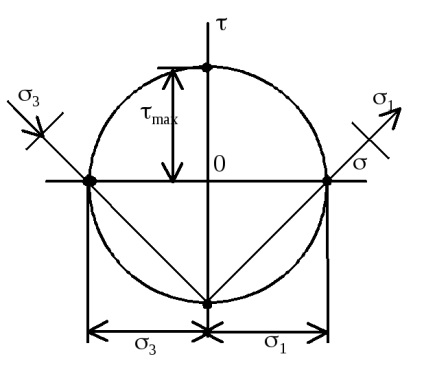
A geometriai jellemzői a sík szakaszok
Terület.
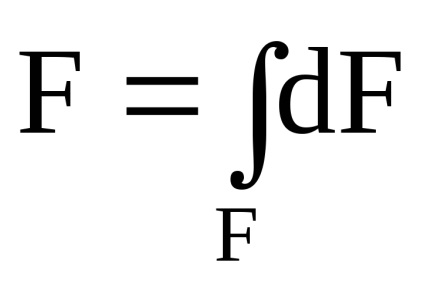
C
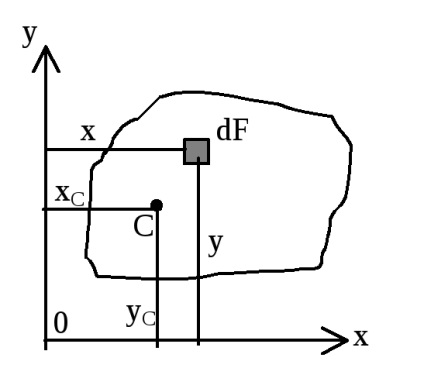
Összefoglalva (integráló) az ilyen munkák az egész számok négyzet kapjunk statikus pillanatok tengelyek körül y és x:

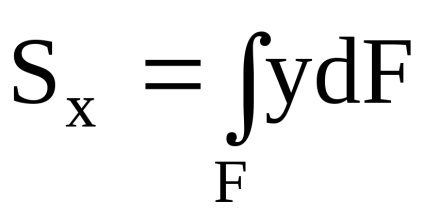
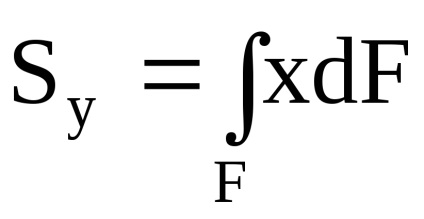
A súlypont koordinátái:
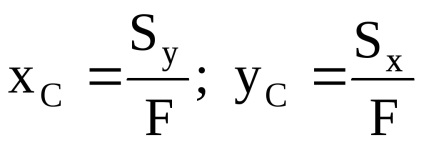
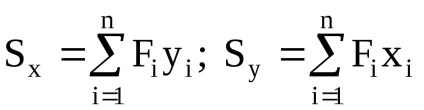
koordinálja a súlypontja egy összetett alak:
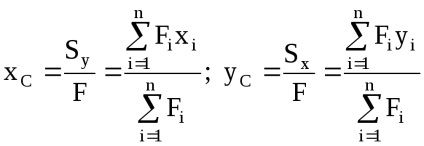
M
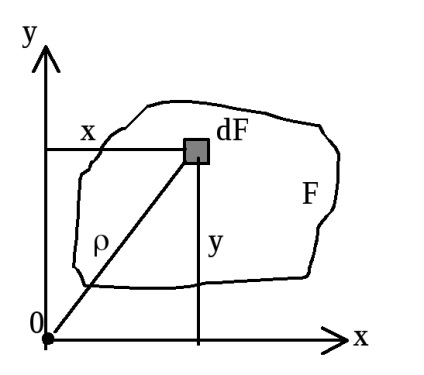
Axial (egyenlítői) tehetetlenségi nyomaték - az értékek összege elemi területek DF négyzetének a távolságok a tengely.
Polar tehetetlenségi nyomaték tekintetében egy pontot (a pólus) - az értékek összege az elemi területek négyzetének távolságok ebben a kérdésben.
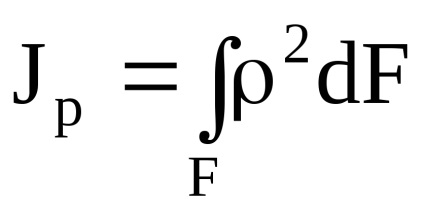
A centrifugális tehetetlenségi nyomaték - az értékek összege az elemi területek azok távolságát két egymásra merőleges tengely.
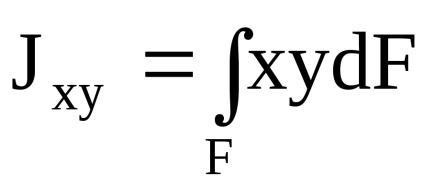
A centrifugális tehetetlenségi nyomaték tengelyek, amelyek közül az egyik vagy mindkettő egybeesnek a szimmetriatengelye, nulla.
Axial és poláris tehetetlenségi nyomatéka mindig pozitív, centrifugális tehetetlenségi nyomatéka lehet pozitív, negatív vagy nulla.
Tehetetlenségi nyomatéka egy komplex szám összege az tehetetlenségi nyomatéka kompozit alkatrész.
Tehetetlenségi nyomatéka egyszerű alak
P
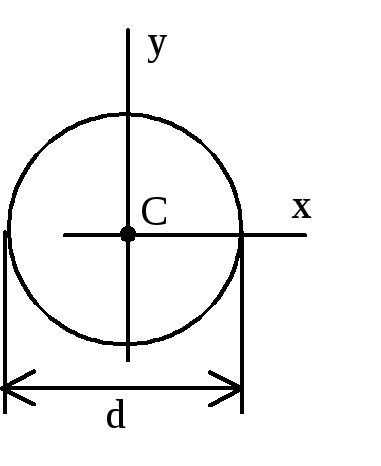
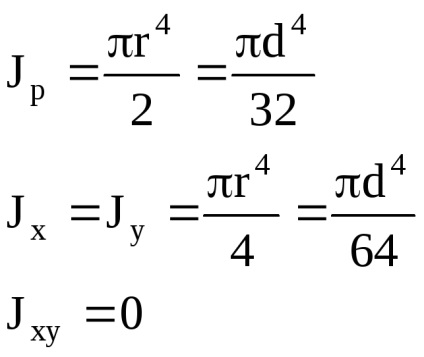
M
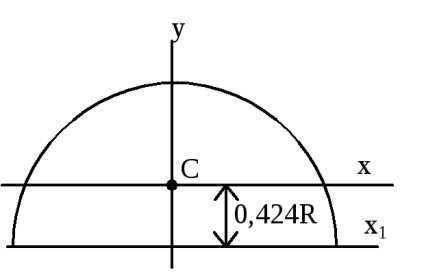
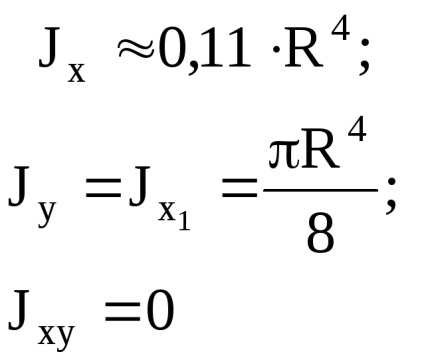
D
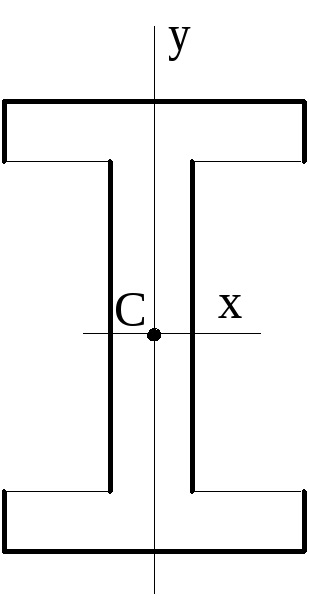
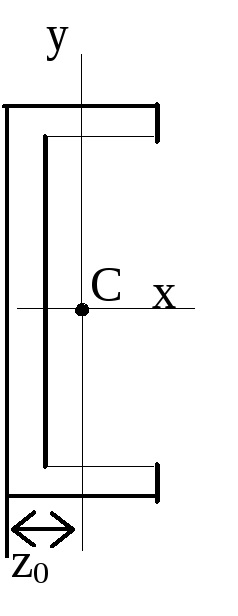
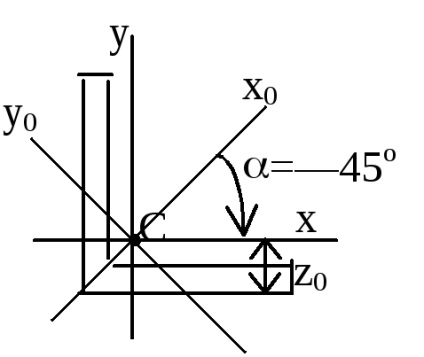
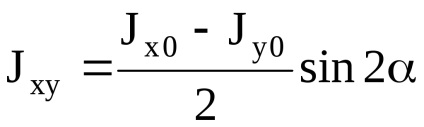
omenty tehetetlenségi párhuzamos tengelyek:
tehetetlenségi nyomaték bármely tengely körüli egyenlő a tehetetlenségi nyomaték egy központi tengely körül ezzel párhuzamosan, valamint a termék a négyzet alakú darabot a négyzetes távolság a tengelyek között. Jy1x1 = Jyx + ABF; ( „A” és „b” helyettesítik be az megadott képlet a jel).
A kapcsolat a tehetetlenségi nyomatékot, amikor fordult tengellyel:
J
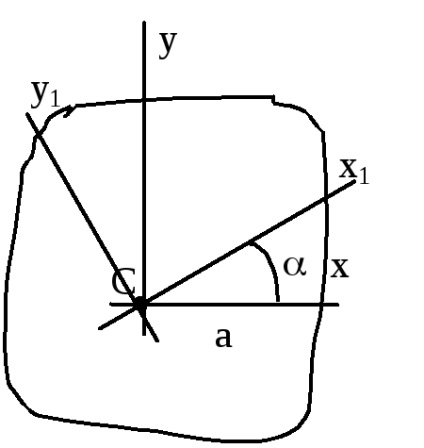
Jx1y1 =
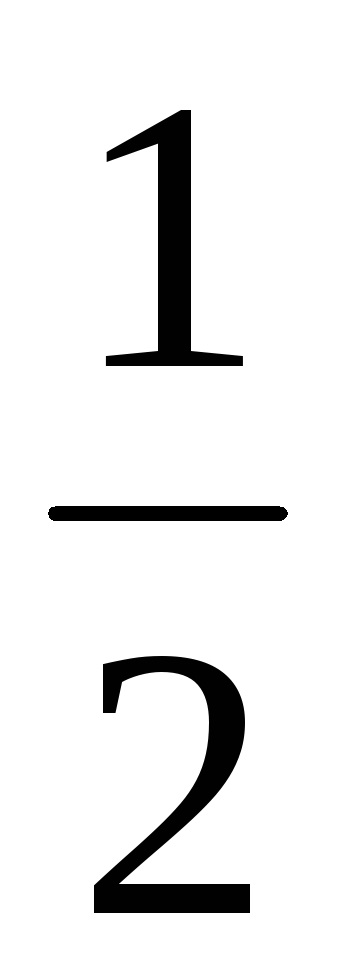
A szög > 0, ha az átmenet a régi és az új koordinátarendszerben fordul ellen chas.str. Jy1 + Jx1 = Jy + Jx
Extrém (minimum és maximum) értékek a tehetetlenségi nyomatékot az úgynevezett fő tehetetlenségi nyomatéka. A tengely körül a tengelyirányú tehetetlenségi nyomatéka szélsőséges értékek, azaz a fő tengelye a tehetetlenség. A fő tengelye a tehetetlenségi egymásra merőleges. Centrifugális tehetetlenségi nyomatékok a fő tengely = 0, azaz, fő tengelye tehetetlenségi - a tengely, amely körül a centrifugális tehetetlenségi nyomatéka = 0. Ha az egyik vagy mindkét tengely egybeesik a szimmetriatengely egybeesik, ők a legfontosabbak. A szög meghatározó helyzetét a fő tengely:
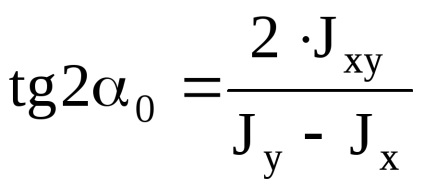
Jmax + Jmin = Jx + Jy. A centrifugális tehetetlenségi nyomaték a fő központi tengelyei tehetetlenségi értéke 0. Ha a fő tehetetlenségi nyomatékok ismertek, az átmenet a képlet forgatjuk tengelyek:
Jx1 = Jmax cos 2 + Jmin sin 2 ; Jy1 = Jmax cos 2 + Jmin sin 2 ; Jx1y1 =
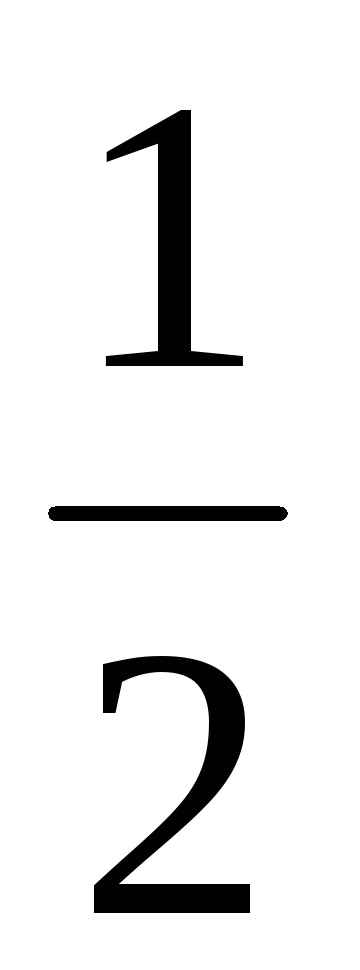
A végső kiszámításakor geometriai jellemzői szakasz célja, hogy meghatározza a fő központi tehetetlenségi nyomatéka és helyzetét a fő központi tengelye tehetetlenség. P
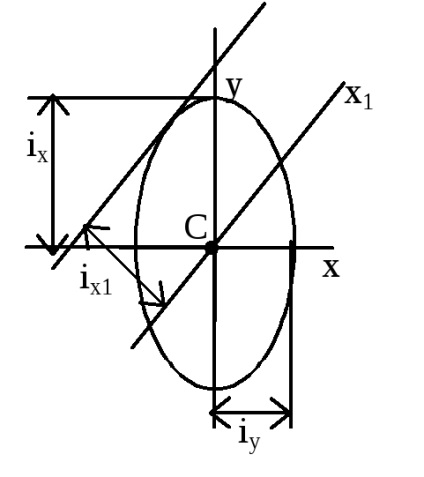
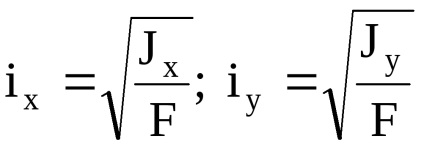
Ha Jx és Jy fő tehetetlenségi nyomatéka, a ix és iy - a fő forgási sugarak. Ellipszis, épül a fő sugara tehetetlensége mind a félig tengely nevezik ellipszis tehetetlenség. Használata az ellipszis tehetetlenségi megtalálható grafikusan ix1 inerciasugara bármely X1 tengely. Erre a célra szükséges felhívni a érintőleges ellipszis párhuzamos x1 tengely. és mérjük meg a távolságot, tengelyen az érintési. Ismerve a forgási sugara, megtalálja a tehetetlenségi nyomaték tengelyére vonatkoztatva X1.