egyenlő megfigyelések
Közvetlen mérések vannak osztva több egyensúlyi és egyenlőtlen. Elméleti alapok és a technika kombinálása mérések eredményeit egyenlőtlen tárgyalja részletesen [3]. Ugyanilyen pontos úgynevezett méréseket segítségével végezzük ugyanazon mérési pontosság az egyik, és az eljárás a Lee állandó környezeti körülmények között. Ha egyformán pontos méréseket MSE eredmények minden méréssorozat egyenlő.
Feldolgozás előtt a mérési eredmények azt kell, hogy megbizonyosodjon arról, hogy az adatokat a feldolgozott minta statisztikailag ellenőrzött, köré csoportosíthatók az ugyanabban a központban, és ugyanazt a szórás. Ellenállás változásokat gyakran értékeljük ösztönösen alapuló hosszú távú megfigyelések. Vannak azonban olyan matematikai módszer, hogy megoldja ezt a problémát - az úgynevezett módszerek homogenitás vizsgálat [3]. Ami a méréseket az egységesség látott csoportok esetekben a szükséges jeleket, amelyek állnak értékelésében elfogulatlan átlag és szórás egymást.
Validation közötti különbségek becslése a varianciák normális eloszlású mérési eredmények által végzett R.Fishera kritériumnak, ha két csoport megfigyelések és M.Bartletta kritériumnak, ha a nagyobb csoportok. Fisher kritériumot figyelembe venni fejezetben. 5.
A feladat feldolgozás eredményeit több mérést, hogy megtaláljuk a becslések és a mért érték a megbízhatósági intervallum, ami a valódi érték. Feldolgozás kell elvégezni összhangban GOST 8,207-76 „GSI. Közvetlen mérések több észrevételt. Feldolgozási módok eredményeinek észrevételeket. Általános rendelkezések”.
Kezdeti információ feldolgozására számos n (n> 4) mérések x1. x2. HG xn. amelyek kizárják ismert szisztematikus hibák - mintavétel. Az n szám függ a követelmények eredmény pontossága, és a valós lehetőségét, hogy végre ismételt mérések.
A szekvenciát feldolgozásának eredményeit direkt mérésekkel a többszörös több szintből áll.
Meghatározása pontbecsléseket mérési eredmények eloszlását. Ebben a szakaszban azt állapítjuk meg:
• a számtani középértéke x a mért érték a képlet (6,8);
• MSE Sx mérési eredményt (6,11), illetve (6.12);
• szórása számtani középérték Sx # 773; a (6.10). A kritériumokkal összhangban tárgyalt Ch. 7, durva hibák és tévedések kiesik, majd újra-számítási becslések számtani átlag és a standard deviáció. Bizonyos esetekben a megbízhatóbb azonosítását a mérések eredményeit a forgalmazási szabályokat lehet meghatározni az egyéb értékelési pont: ferdeség, csúcsossága és kontrekstsess, az entrópia aránya.
Meghatározása a törvény eloszlása a mérési eredményeket vagy véletlenszerű mérési hibákat. Az utóbbi esetben a minta mérési x1. x2. x3 -. xn visszük át mintát eltérések számtani átlaga DH1. DH2. DH3. DHN. ahol Dxi = xi - x # 773;.
Az első lépés azonosítása az elosztási gyakorlat az, hogy létrejöjjön a korrigált mérési eredmények xi. ahol i = 1, 2 N, variáció sorozat (rendelt kiválasztási) és yi. ahol yi = min (xi) és yn = max (xi). Számos változatban a mérési eredmények (vagy eltérés a számtani átlag) vannak elrendezve növekvő sorrendben. Továbbá, ez a tartomány van osztva az optimális m számot, általában azonos csoportosítása időközönként hosszúságú h = (y1 + yn) / m.
A probléma meghatározása az optimális m számú időközönként csoportosítás venni számos tanulmány, összefoglalva [4]. Az optimális érték intervallumok számát m, ahol a lehetséges maximális adatok simító véletlenszerű ingadozás kíséretében minimális torzítás a simítás a görbe maga a kívánt eloszlást. Gyakorlati alkalmazásra célszerű a javasolt felhasználási a [4] expressziós M min = 0,55n 0,4 és M max = 1,25n 0,4. állítjuk elő a leggyakrabban előforduló a gyakorlatban eloszlásokkal kurtosis tartományban van a 1,8-6, azaz Az egységes a Laplace eloszlás.
A szükséges m értéke legyen a hatótávolság akár mmjn Mmax. lehet páratlan, mint abban az esetben egy még m csúcsosság szimmetrikus eloszlását vagy bimodális hisztogram a központban két oszlop azonos magasságú, és egy középső eloszlási görbét mesterségesen lapított. Ha egyértelműen bimodális hisztogram, az oszlopok száma növelhető 1,5-2-szer mindkét csúcs elszámolt mintegy méterenként. A kapott érték a csoportosító intervallum hossza h mindig lekerekített felfelé, egyébként az utolsó pont kívül esik az extrém tartományban.
További csoportosítás meghatározott időközönként kísérleti adatok, mint a D1 = (Y1 Y1 + H.); D2 = (y1 + H, Y1 + 2H);. ; Dm = (yn - H; in), és számolja a találatok száma nk (frekvencia) A mérési eredmények az egyes csoportokat intervallumban. Az összeg ezen számok egyenlőnek kell lennie a dimenziók száma. A kapott értékek kiszámítása a valószínűsége, hogy a mérések eredményeit (relatív frekvenciák) az egyes csoportokat időközönként képletű pk = nk / n, ahol k = l, 2 m.
A számítások lehetővé teszik, hogy állítson össze egy hisztogram, sokszög és a kumulatív görbe. A konstrukció egy hisztogram, az eredmények a megfigyelések X tengely (ábra. 8.1, a) letétbe Dk időközönként növekvő sorrendben és az egyes intervallumok épített téglalap magassága pk. A körülzárt terület a diagram alatt, Arányos / ionalna n megfigyelések száma. Néha, a magassága a téglalap feküdt empiricheskoy változó valószínűségi sűrűség pk = Pk / Dk = NK / (NDK), amely a becsült átlagos sűrűsége a tartományban Dk. Ebben az esetben a terület a hisztogram egyenlő eggyel. Számának növelésével az intervallumok és ennek megfelelően csökkenti a hosszuk hisztogram egyre közeledik egy sima görbe - a valószínűség-sűrűség grafikonon. Meg kell jegyezni, hogy bizonyos sluyaaev termelni becsült kiegyenlítő a hisztogram, amely azt mutatja, a technika [4]
A sokszög egy sokszögű összekötő görbe a középső felső alapjából Minden hisztogram oszlopon (lásd. Ábra. 8.1, a). Ez világosabban, mint a hisztogram tükrözi eloszlás alakja görbe. Kívül a hisztogram a jobb és a bal oldalon van az üres helyekkel, amely pontot megfelelő a felezőpontja fekszenek az x tengelyen.
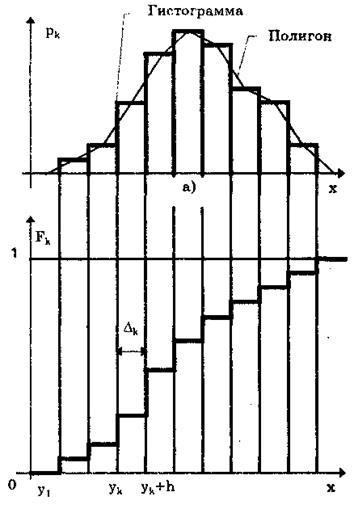
Ábra. 8.1. Gistonramma, sokszög (a), és a kumulatív görbe (b)
Ezek a pontok, ha építési sokszög által összekötött egyenes szakaszokkal. Ennek eredményeként, valamint a X-tengely, zárt alakú, egy terület összhangban normalizálási szabálynak egyenlőnek kell lennie az egység (vagy a megfigyelések száma használatával a relatív frekvenciák).
A kumulatív görbe - egy grafikon, a statisztikai eloszlás függvények. A konstrukció tengelyirányban megfigyelések x (ábra. 8.1,6) feküdt Dk időközönként növekvő számsorrendben és építeni minden intervallum téglalap magassága
Fk érték az úgynevezett kumulatív relatív gyakorisága és mennyisége nk - összegzett gyakoriság.
Típusa szerint kirajzoló tehető forgalmazás joga a mérési eredményeket.
Értékelése a megoszlása a törvény statisztikai kritériumok alapján. Ha az n szám> 50 megfigyelések azonosítani az elosztó törvény Pearson-féle teszt (chi-négyzet cm. 8.1.2), vagy Mises kritérium-Smirnov (w2). A 50> n> 15 ellenőrzéséhez eloszlásának normalitását törvény alkalmazása egy összetett kritériumot (d-teszt) megadott GOST 8,207-76. Az n <15 принадлежность экспериментального распределения к нормальному не проверяется.
Meghatározása konfidenciahatárait véletlen hiba. Ha azonosítani tudja a forgalmazási jog mérési eredmények felhasználásával azt a kvantilis zp tényezőt egy adott érték megbízhatósági valószínűség P. Ebben az esetben a konfidenciahatárait véletlen hiba A = ± zp S -.
Meghatározó a határokat, nem kizárt a szisztematikus hiba q mérési eredményt. Ilyen határok eredmények észre nem statisztikai módszerekkel intervallum határait, amelyen belül egy Maradék hiba. Ez van kialakítva alkatrészek száma: jellemzően, a módszer és a hiba mérő eszközökkel, és a szubjektív hiba. Átnyúló nem kizárt a szisztematikus hiba veszik, hogy a határ az elfogadható alap- és járulékos hiba mérőműszerek, ha azok véletlen komponensek elhanyagolható. Ezek össze szabályai szerint tárgyalja Sec. 9.2. Megbízhatósági szint meghatározásakor határait 6 egyenlőnek kell lennie a megbízhatósági szintet használják megtalálni a véletlen hiba határokat.
Meghatározása konfidenciahatárait mérési hiba eredményezheti Dp. Ez a művelet úgy hajtjuk végre, hogy az szórása véletlen komponens Sx # 773; és a határok Maradék komponens q arányától függően a Q / Sx # 773; szabályok szerint meghatározott szakasz. 9.4.
Menteni egy mérési eredményt. A mérési eredmény van írva a x = x # 773; ± Dp megbízhatósági szinten a P = P hiányában egy adat hiba komponensek az eloszlási függvény a mérések formájában x, S-, N, 8 megbízhatósági szinten a P = Pd.