Centripetális gyorsulás elmélet és online kalkulátorok
Centripetális gyorsulás a kerületen egyenletes mozgás
Hagyja, hogy a anyagi pont mozog egyenletesen egy kört. Akkor a modul nem változik a sebessége ($ v = const $). De ez nem jelenti azt, hogy a gyorsulás egy anyagi pont nullával egyenlő. A sebességvektor érinti a mozgási útvonalát pont. Ha mozog a kerülete sebesség iránya változik folyamatosan. Tehát a lényeg felgyorsul.
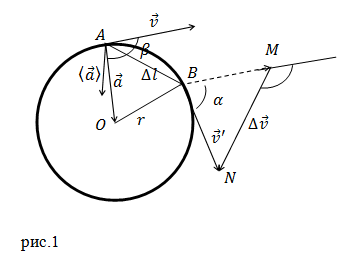
Tekintsük az A és B pontok tartozó pályáját a test mozgásban van. Sebességvektor változások ezek a pontok egyenlő:
Ha a mozgás között A és B pontok kicsi az AB ív alig különbözik a húrt AB. BMN háromszög AOB és hasonló, így:
átlagos gyorsulás modul található, mint:
A pillanatnyi gyorsulás érhető el megy a határ, mint $ \ Delta t \ 0 \ $ a $ \ left \ Langle alagútrendszert a \ right \ rangle $:
A vektor átlagos gyorsulás és sebesség vektor szög egyenlő:
Ha $ \ Delta t \ 0 \ angle $ $ \ alpha \ 0. $ kiderül, hogy a pillanatnyi gyorsulás vektor egy sebességvektor szög $ \ frac $.
Azt találtuk, hogy egy anyagi pont, mozgó egységesen kör, felgyorsul közepe felé az út a mozgás (merőleges a sebességvektor), annak nagysága egyenlő a sebesség négyzet osztva a kör sugara. Ez a gyorsulás az úgynevezett centripetális vagy normális. jelzik ez általában $ _n $.
ahol $ \ omega $ - szögsebessége a mozgását egy pont ($ v = \ omega \ r cdot $).
Meghatározása centripetális gyorsulás
És így, a centripetális gyorsulás (általában) - egy összetevő a teljes gyorsulás az anyag pont, amely jellemzi, hogy milyen gyorsan megváltoztatja az irányát a sebesség vektor a görbe vonalú mozgását. Egy másik összetevője a teljes gyorsulás a tangenciális gyorsulás, ez felelős a változás nagysága a sebesség.
Centripetális gyorsulás:
ahol $ e_r = \ frac> $ - egység vektor irányított a görbületi középpontja a pálya a kérdéses pont.
Először megfelelő képlet a centripetális gyorsulás Huygens kaptunk.
A mértékegység a centripetális gyorsulás Nemzetközi Mértékegységrendszer méter osztva második négyzeten:
Példák problémák megoldás
Feladat. A korong körül forog rögzített tengely. A törvény megváltoztatja a méretét, a lemez forgási szög a következő egyenlet adja: $ \ varphi = 5t ^ 2 + 7 \ (rad) $. Mi a centripetális gyorsulás A meghajtó pont, amely a parttól $ r = $ 0,5 m-re a forgástengely a végén a negyedik másodpercben a forgatás kezdetétől?
Határozat. Készíts egy rajzot.
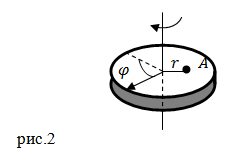
Modul centripetális gyorsulás:
Szögsebesség pontot találtam:
Az egyenlet megváltoztatja a forgatás szögét, attól függően, hogy az idő:
A végén a negyedik második szögsebesség:
\ [\ Omega \ left (t = 4 \ right) = 10 \ cdot 4 = 40 \ \ left (\ frac \ jobbra). \]
Kifejezést használja (1.1), azt látjuk, a nagysága a centripetális gyorsulás:
Feladat. A mozgás az anyag pont a következő egyenlet adja: $ \ overline \ left (t \ right) = 0,5 \ (\ overline \>) $, ahol $ \ omega = 2 \ \ frac $. Mi a nagysága a normál gyorsulás értelme?
Határozat. Ennek alapján a probléma megoldására kerül meghatározása centripetális gyorsulás formájában:
Úgy látszik az a feladat feltételei, hogy a pálya a mozgás egy pont egy kör. A paraméteres egyenlet a következő formában: $ \ overline \ left (t \ right) = 0,5 \ (\ overline \>) $, ahol $ \ omega = 2 \ \ frac $ is képviselteti magát:
A sugara a pálya lehet meghatározni:
A sebesség komponensek:
Vevőmodullal sebesség:
Helyettesítő érték sebesség és kör sugarát a kifejezést (2.2), van: