Az ingatlan az érintő és metsző háromszögeket
A tétel a arányossági szegmensek metsző és tangens
(Ingatlan érintő és metsző végzett egy ponttal)
A tangens és metsző egy körbe lefolytatott egyik pontról, a négyzetes távolság ezen a ponton a tapintási pont megegyezik a termék hossza mentén szekáns a külső rész hossza.
Más szóval, a távolság négyzetével ettől a ponttól az érintkezési pont megegyezik a termék a távolságokat ettől a ponttól a metszéspontok egy metsző körrel.
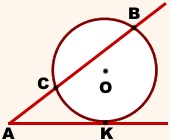
Tekintettel. env. (O; R), AK - tangens, AB - szekáns
env. (O; R) ∩AK = K, (O; R) ∩AB = B, C
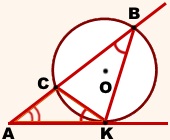
Tekintsük a háromszög ABK és AKC.
Ezek ∠A - összesen.
(A bezárt szög. CK alapuló ív).
Ezért Háromszögmódszert ABK és AKC hasonló (két sarkok).
A hasonlóság háromszögek arányosnak kell lennie az illető felek:
Az alapvető tulajdonsága aránya
QED.
A középpontú kör oldalán háromszög AC ABC áthalad a C csúcsánál, és érintkeznek AB vonal a B pontban Find AC, ha a kör átmérője egyenlő 15, és az AB = 4.
ΔABC, B, C ∈ env (O; R). O∈AC, AB - tangens, AB = 4, FC - átmérőjű FC = 15
By ingatlan érintő és metsző végzett egy pont,
Legyen AF = x, akkor AC = x + 15. Összetétele és megoldani az egyenletet:
A második gyökér nem megfelelő értelmében a problémát. Következésképpen, AC = 1 + 15 = 16.