Az elmélet szerint a valószínűség - ellenőrzési munka
1. A fehér doboz a 2 és 4 fekete golyót. Egyenként eltávolították a golyó benne. Annak a valószínűsége, hogy az utolsó labdát fekete.
Jelöljük: A - az esemény, amikor a tényt, hogy az utolsó labdát húzott egy doboz - fekete.
Annak a valószínűsége, a vizsgálat abban a tényben rejlik, hogy az utóbbi nyerjük labda - fekete, talán a leggyakrabban teszt kivonat a fiókból a labdát:
Aztán ez a teszt 6 egyformán valószínű eredmények :.
Ezeknek elemi esemény kedvező eredményt.
Ezután a fogalom klasszikus valószínűség, van:
- annak valószínűsége, hogy az utóbbi behajtott a labda fekete lesz.
2. A szállítmány, amely 30 férfi kabátok, több mint 20 helyszínen előállított termékek. Áruk véletlenszerűen kiválaszt három terméket. Mi a valószínűsége annak, hogy mind a három termék lesz:
a) a helyi termelés; b) a helyben nem termelt.
a) Annak a valószínűsége, hogy a 3 a kiválasztott terméket, mindhárom fogják helyben előállított,
találjuk a következő képlet szerint:
- hányféleképpen lehet eltávolítani 3 elem a helyi termelés 20 (ez a kedvező eredmény)
- - hányféleképpen amit tud kivonat 3 termék 30, (ez az összes lehetséges kimenetelt).
Aztán. - annak a valószínűsége, hogy a 3 kiválasztott elemek, mind a három kerül a helyben termelt.
b) Annak a valószínűsége, hogy a 3 a kiválasztott terméket, mind a három nem lesz a helyi termelés,
találjuk a következő képlet szerint:
- hányféleképpen amit tud kivonat 3 termék nem helyi termelés 30-20 = 10 (ez a kedvező eredmény)
- - hányféleképpen amit tud kivonat 3 termék 30, (ez az összes lehetséges kimenetelt).
Aztán. - annak a valószínűsége, hogy a 3 kiválasztott elemek, mind a három nem lesz helyi termelés.
3. Statisztikák kölcsön kéri a bank a következő: 10% - az állami szervek, 30% - más bankok, mások - magánszemélyek. Valószínűsége alapértelmezett hitel vesszük, mint a következők: 0,01, 0,05 és 0,2. Keresse meg a nemteljesítési valószínűség a következő kérés kölcsön. Credit Osztály vezetője számolt be, hogy megkapta az üzenetet a kölcsön alapértelmezett, de a hasonmás üzenetet az ügyfél neve olvashatatlan. Mi a valószínűsége annak, hogy a hitel nem ad vissza semmilyen bank?
Jelöljük az esemény „a kölcsönt nem tért vissza”
H1 - a kölcsönt nem állami szervek iránt.
H2 - a kölcsönt nem tért vissza semmilyen bank.
H3 - a kölcsönt nem tért vissza az egyének.
A valószínűségek a hipotézisek H1. H2 és H3 szerinti állapotát, amelyek
Feltételes valószínűség az esemény egy ezen a hipotéziseket szerint paribus
Akkor használjuk a képlet teljes valószínűség:
- a valószínűsége a hitel nem kerül visszafizetésre.
Annak a valószínűsége, hogy a hitel még nem tért vissza a bankok, azt látjuk, a Bayes formula:
4. Mi a valószínűsége, hogy legalább két hatos, három dob a kocka?
Jelöljük az esemény „a kocka esett 6 pont”
Annak a valószínűsége, ez az esemény határozza meg a következő képlet szerint:
, ahol - több, egyformán lehetséges kimenetelek (veszteség 1,2,3,4,5 és 6 pont). - A kedvező esetek száma (veszteség 6 pont).
Veszteség három dob legalább két hatos elvesztését jelenti, két vagy három hatos.
Szerint a kiegészítéssel tétel:
Ahhoz, hogy megtalálja a valószínűsége, hogy két és három hatos három dob a kocka, használja a Bernoulli formula
valószínűsége visszatérő események:
Majd: - a valószínűsége, hogy legalább két hatos, három dob a kockával
5. Csírázás A mag a növény 0.9. Annak a valószínűsége, hogy ki a 900 magot ültetett: a) hajtás pontosan 700; b) a száma kicsírázott közötti 790 és 830.
a) Mekkora a valószínűsége, hogy pontosan 700 magvak:
Az általunk használt helyi Laplace-tétel:
és lehet tekinteni,
Ie valószínűsége esemény, hogy a 900 ültetett magok kihajtanak pontosan 700, közel nulla.
b) annak a valószínűsége, hogy a szám a csíráztatott magok között fekszik 790 és 830:
On állapot: - annak a valószínűsége, csírázási,
Mivel az értékek és a nagy, akkor használja a Csebisev egyenlőtlenség:
Annak a valószínűsége, hogy az eltérést egy véletlen változó matematikai elvárás kevesebb, mint néhány szám:
Határérték szimmetrikus, tehát ettől az egyenlőtlenség lépni a egyenlőtlenség
Vagy hasonlítsuk össze és kap:
Az érték a következő képlettel: ahol
6. A befektető vásárol értékpapírokat a kölcsön venni a kamatláb r jelzálog. A kamatlába értékpapírok X - valószínűségi változó MX = a, a> r, DX =
a) a regressziós módszer határozza meg a képzési idő szükséges egy új alkalmazott, a 30 éves kort.
Jelöljük - alkalmazott életkor - az előállítás időpontjában
b) meghatározzuk a korrelációs koefficiens az alábbi képlet szerint:
- korreláció pillanatban jellemzi a következő egyenlet:
Elvárások és a következőképpen definiált:
Aztán összefüggés pillanatban:
A korrelációs együttható értéke nullától eltérő, ezért az értékek korrelálnak.
9. átvétele biztosítási díjak a 130 ágak biztosító társaságok a régióban A volt 26 x 104. e. a régióban elszámolt 18 · 104 100 ágra. e. A diszperzió értéke a biztosítási díjak a régióban A jelentése megegyezik a 39 x 108 (a. e.) 2. A régióban - 25 · 108 (. cu.) 2. Szignifikancia szinten a = 0,05, meghatározza, hogy jelentősen eltérő átlagos értéke nyugták a biztosítási díjak az A és B tartományok alapján 1 ág.
By hipotézis, tudjuk, hogy a következő információkat:
Annak érdekében, hogy egy adott szignifikanciaszint, hogy teszteljék a nullhipotézis egyenlőség elvárásait két normális eloszlású populáció, úgy kell számítani a megfigyelt értéke a vizsgált:
És Laplace függvénytábla, hogy megtalálják a kritikus pont az egyenlőség
Ha - nincs ok arra, hogy elvetjük a nullhipotézist.
Ha - elvetjük a nullhipotézist.
Mi először meghatározza a közép- és
Segítségével Laplace táblázat segítségével határozza meg a kritikus pont:
És összehasonlítjuk. kapjuk:
Tehát, nincs ok, hogy elutasítja azt a hipotézist, hogy az egyenlő a várakozások adateloszlások.
Az eltérés tehát az átlagok bevételek biztosítási díjak az A és B tartományok alapján ág 1 nem lényeges.
Válasz. átlagos bruttó beáramlás a biztosítási díjak
Ezek nem különböznek jelentősen
10. Az autókölcsönző cég érdekelt a kapcsolatát futásteljesítmény járművek (A) és az értéke a havi karbantartási (Y). 15 autó került kiválasztásra, hogy meghatározzák a természet ezt a kapcsolatot.
Ábrázoljuk a nyers adatokat, és meghatározza a jellegét annak függvényében. Számítsuk ki a szelektív Pearson lineáris korrelációs együttható, ellenőrizze annak jelentőségét a = 0,05. Build a regressziós egyenletet, és így az eredmények értelmezése.
A grafikon a nyers adatok:
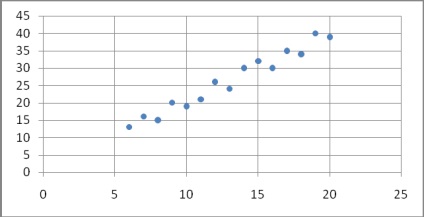
Mint látható a grafikonon, a kapcsolat a értékek X és Y lehet venni, mint a lineáris.
Szelektív Pearson korrelációs együttható a lineáris