Az egyenletek az érintő és a normális
Az egyenlet az érintő derékszögű koordináta
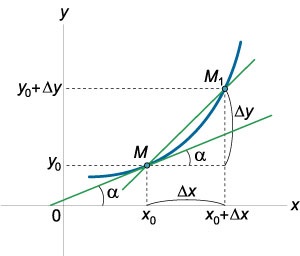
Tegyük fel, hogy a függvény \ (y = f \ left (x \ right) \) van definiálva az intervallum \ (\ left (\ right) \) folytonos a ponton \ (\ a \ left (\ jobbra). \) Ebben a (a pont \ (M \) az ábrán \ (1 \)) értéke \ (= f \ left (> \ jobbra). \)
Legyen a független változó a ponton \ (\) értékkel növekszik \ (\ Delta x \.) A megfelelő növekmény függvény \ (\ Delta Y \) adják \ [\ Delta y = f \ left (+ \ Delta x> \ jobbra) - f \ left (> \ jobbra). \] ábra \ (1 \) pont \ (\) a koordinátái \ (\ left (+ \ Delta X, + \ Delta y> \ jobbra). \) konstrukció szekáns \ ( M. \) egyenletét a forma \ [y - = k \ bal (> \ jobbra), \] ahol \ (k \) - szögletes együttható függően növekmény \ (\ Delta x \) és egyenlő a \ [k = k \ left (\ right) = \ frac >> \] Amikor csökkenti a \ (\ Delta x \) pont \ (\) hajlamos arra, hogy a pont \ (M: \). \ (\ M. \) a határérték \ ( \ Delta x \ 0 \), a pontok közötti távolság \ (M \) és \ (\) nullához. Ez következik a folytonosság függvény \ (f \ left (x \ right) \) azon a ponton, \ (: \) \ [\ Delta y = 0,> \; \; \ Left |> \ right |> = \ sqrt \ right)> ^ 2> + \ right)> ^ 2 = 0. >>> \] korlátozó helyzetében a szelő \ (M \) csak képviseli az érintő a grafikon függvény \ (y = f \ left (x \ right) \) azon a ponton, \ (M. \)
Kétféle érintők - ferde és függőleges.
Definíció \ (1 \).
Ha van egy véges határérték \ (\ lim \ limits_ k \ left (\ right) =, \), akkor az egyenes vonal, melynek egyenlete \ [y - = k \ bal (> \ jobbra), \] úgynevezett ferde érintő a grafikon a \ ( y = f \ left (x \ right) \) azon a ponton, \ (\ left (,> \ jobbra). \)
2. Definíció.
Ha a határérték \ (k \), ha a \ (\ Delta x \ 0 \) végtelen: \ (\ lim \ limits_ k \ bal (\ right) = \ pm \ infty, \), akkor az egyenes vonal, melynek egyenlete \ [ X =, \] nevezzük húzott függőleges érintő a grafikon a \ (y = f \ left (x \ right) \) azon a ponton, \ (\ left (,> \ jobbra). \)
Fontos, \ [= \ lim \ limits_ k \ bal (\ right)> = \ frac >>> => \ jobbra),> \] vagyis a meredeksége az érintő vonal értékével egyenlő differenciálhányados \ (f \ balra (> . \ right) \) át az érintési pont \ (\) Ezért az egyenlet ferde tangens lehet ebben a formában íródott: \ [= f „\ left (> \ right) \ left (> \ right) \; \; \ text> \ ; \ ;.> \ right) \ left (> \ jobb) + f \ bal (> \ right)> \], mivel a vonal meredekségét egyenlő a lejtőn a \ (\ alpha, \), amely vonal teszi a pozitív irányát az x-tengelyen , akkor a következő terner egyenletet: \ [k = \ tan \ alpha = f „\ left (> \ right) \.]
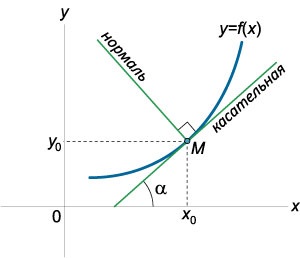
Normál egyenlet derékszögű koordináta
Egy egyenes merőleges az érintő és átmegy az érintkezési ponton \ (\ left (,> \ jobbra), \) az úgynevezett normális, hogy a grafikon a \ (y = f \ left (x \ right) \) ezen a ponton (ábra \ (2 \ )).
A ismert geometriájú, hogy a termék a szögletes együtthatók a vonalak merőleges \ (- 1 \) Ezért, ismerve az egyenlet az érintő a ponton \ (\ left (,> \ jobbra): \) \ [y - = f „\ left (> \ jobbra) \ left (> \ right) \] akkor azonnal írja le az egyenletet a szokásos formában \ [y - = -. \ frac> \ right) >> \ left (> \ right) \]
Egyenletek érintő és normális paraméteres alakban
Érintő és normál egyenletek polár-koordinátákkal
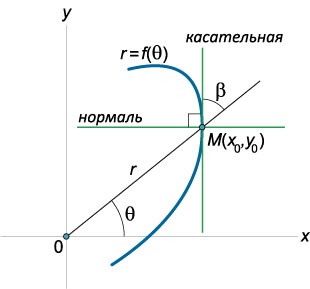
Tegyük fel, hogy a görbe az adott egyenlete polárkoordináták \ (r = f \ left (\ theta \ jobbra), \) kifejező függését a sugár vektor hossza \ (r \) a poláris szög \ (\ theta. \) A derékszögű koordináták, egy görbe lesz által leírt egyenletrendszert \ [\ left \<\begin x = r\cos \theta = f\left( \theta \right)\cos \theta \\ y = r\sin \theta = f\left( \theta \right)\sin\theta \end \right..\] Таким образом, мы записали уравнение кривой в параметрической форме, где роль параметра играет угол \(\theta.\) Далее легко получить выражение для углового коэффициента касательной, проведенной к кривой в точке \(\left( ,> \ Right): \) \ [>>>>> = \ right)> ^ \ prime >>> \ right)> ^ \ prime >>>> = \ sin \ theta + r \ cos \ theta >> \ cos . \ theta - r \ sin \ theta >>> \] Ennek eredményeként, az érintő és a normál egyenlet lesz írva a következő formában: \ [= \ frac >>>> \ left (> \ right)> \; \; \; ),> \] \ [= - \ frac >>>> \ left (> \ right)> \; \; \; ).> \] Tanulmány a görbe végezhetjük közvetlenül polárkoordináták átmenet nélkül egy Descartes-rendszer. Ebben az esetben, az érintő lejtő szöge, amelynek meghatározása nem \ (\ theta \) a sarki tengely (vagyis a pozitív irányát az x-tengely irányában), és a szög \ (\ beta \), hogy a vonal, amely a sugár vektor \ (r \) (ábra \ (3 \)).
A parabola egyenlet által definiált \ (y = + 2x + 3 \) létrehozása egyenlet érintő a parabola, ponton áthaladó \ (A \ left ( <- 1,1> \ Right). \)
Transzformációs egyenlet a parabola jelenti \ [+ 2x + 3> = + 2x + 1 + 2> = \ right) ^ 2> + 2> \] Látható, hogy a grafikon a parabola nyerik a grafikont a funkció \ (y = \) a eredmény párhuzamos közlekedés \ (1 \), és az egyik, hogy a balra a \ (2 \) egység (ábra \ (7 \)).
Találunk az egyenlet a két érintő a parabola, ponton áthaladó \ (A \ left ( <- 1,1> . \ Right) \) Mindegyik érintők egyenlet által definiált \ [= k \ left (> \ right),> \; \; \ Jobb)> \ right),> \; \; \; \; \] Ahol \ (k \) - a meredekség (\ (\) - az első érintő és \ (\) - a második).
Így a probléma csökkenti, hogy meghatározzuk a lejtőn a tangens \ (\) és \ (. \) Vegye figyelembe, hogy a pontok érintési \ (B \) és \ (C \) állapotban \ [y = kx + k + 1 \\ y = + 2x + 3 \ end \ jobbra,> \ ;. \; + 2x + 3.> \] Továbbá, a érintési pontok \ (B \) és \ (C \) meredeksége értéke differenciálhányados \ (y = + 2x + 3. \) Mivel \ [+ 2x + 3> \ right) ^ \ prime >> = \], majd ennek következtében azt, hogy egy másik egyenlet formájában \ [k = 2x + 2 \] Ennek eredményeként, van egy rendszer két egyenlet \ [\ left \<\begin kx + k + 1 = + 2x + 3\\ k = 2x + 2 \end \right.\] с двумя неизвестными \(k\) и \(x.\) Решая эту систему, находим значения \(k\) и \(x\) (т.е. угловые коэффициенты касательных \(,\) \(\) и абсциссы точек касания \(B\) и \(C\)): \[ kx + k + 1 = + 2x + 3\\ k = 2x + 2 \end \right.,>\; \; \ Right) x + 2x + 2 + 1 = + 2x + 3> \; \; + 2x + 2x + 3 = + 2x + 3> \; \; + 2x = 0,> \; \; = - 2 \; = 0.> \] Az első döntést \ (= - 2 \) megfelel pont \ (B. \) második megoldás \ (= 0 \) az a koordináta a tapintási pont \ (C \) szögletes együtthatók értékei a következők:-
tangens \ (AB: \; \) \ (y = -2x - 1; \)
tangens \ (AC: \; \) \ (y = 2x + 3 \)
Ahhoz, hogy egy grafikon, a \ (y = \ cos x \) tartott érintőjének ponton \ (M \ left (,> \ jobbra), \), ahol \ (0 0, \] a származék csak egy kritikus pont, amely állapota által meghatározott \ [Z = 0,> \; \; \ right) = 0,> \; \; \] Ezt az egyenletet numerikusan megoldható. Azonban látható, hogy ha a \ (z = \ nagy \ frac \ normalsize, \), majd a bal oldalon az egyenlet negatív: \ [:> \; \; - \ gyermekágy \ frac> = - 1 \ kb - 0,21 0.> \] Következésképpen, az a pont szélsőérték függvény \ (S \ left (z \ right) \) van a szög intervallumban \ (\ left (\ normalsize, \ nagy \ frac \ normalsize> \ right) \) (ábra \ (12 \)), és ezen a ponton a minimális pont (természete szerint a deriváltja elõjelet).
A közelítő koordinátáit a minimális pont lehet kiszámítani, például az Excel. Ez körülbelül \ (0,86 \; \ text \) vagy a \ (49,3 ^ \.)

Kapcsolódó cikkek