Atelny (exponenciális eloszlás jog)
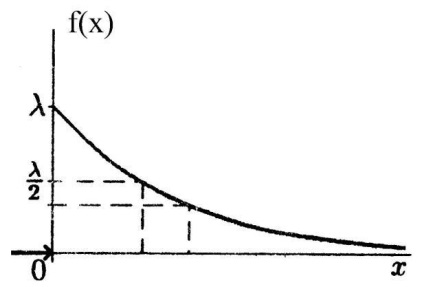
Az X valószínűségi változó elosztva az exponenciális eloszlás törvény paraméterrel λ. ha sűrűségfüggvénye adja meg:
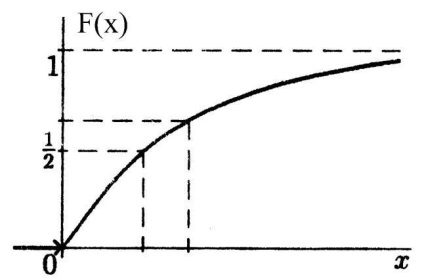
Az eloszlásfüggvény:
A várható értéke és szórása egy véletlen változó szerint szét kell exponenciális törvény által adott:
Azt találtuk, hogy a javítási idő a TV egy véletlen változó X. elosztott exponenciálisan.
Határozzuk meg annak a valószínűsége, hogy a TV javítás lesz szükség, legalább 20 nappal, ha az átlag javítási idő TV 15 nap. Annak a valószínűsége, sűrűség eloszlás, és a standard eltérés a véletlen változó X.
A hipotézis, a várakozás M (x) = 1 / λ = 15, ahol a paraméter λ = 1/15. Ezután a sűrűségfüggvény és az elosztási formájában fog:
Kívánt valószínűsége P (X ≥20) megtalálható a képletből, integrálásával a valószínűsége sűrűsége, azaz a
de könnyebb, hogy ezt az eloszlásfüggvény:
Azt találjuk, az átlagos eltérés: σ (X) = M (X) = 15 nap.
3.Ravnomerny forgalmazási szabályokat.
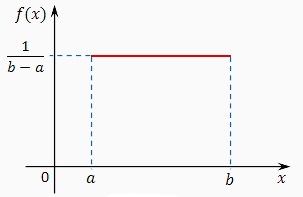
Folyamatos X valószínűségi változó egyenletes eloszlása törvény (a törvény állandó sűrűségű) a szegmens [a; b], Ha ezen a ponton a valószínűségi változó sűrűségfüggvénye konstans, azaz a
Ennélfogva, a várakozás egy valószínűségi változó egyenletes eloszlású az intervallum (a. B), egyenlő a középső és ezen intervallum.
A variancia a következő:
Találunk a valószínűsége értékű valószínűségi változó, amelynek egyenletes eloszlású intervallum tartozó teljes intervallum [a. b]:
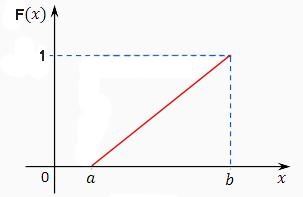
Az eloszlásfüggvény formájában:
Metro vonatok rendszeresen időközönként 2 percig. Az utas belépett az emelvényt véletlenszerű időben. Mi a valószínűsége annak, hogy az utas meg kell várni, nem több, mint fél perc.
Az átlag és a szórás egy X valószínűségi változó - a várakozási idő a vonat.
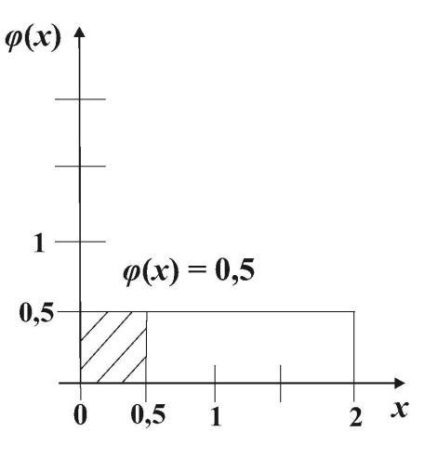
A valószínűségi változó X - egy vonat várakozási időt az idő (perc) a [0, 2] egy egyenletes eloszlású törvény f (x) = 1/2.
Ezért a valószínűsége, hogy az utas meg kell várni, nem több, mint fél perc egyenlő 1/4 részét egy téglalap területét egyenlő egység, azaz a
Találunk a várható értéke és szórása a szórás:
12. Chance meghatározott változása. Három szigma szabály.
Tétel. Valószínűsége modul eltérése folytonos X valószínűségi változó a matematikai elvárás az értéke egy tetszőlegesen kis számú ε> 0 képlet adja meg:
(*)
Szabály három szigma.
Behelyettesítve az értéke ε a (*), kapjuk:
Tehát valószínűséggel tetszőlegesen közel van az egység lehet azzal érvelni, hogy a készülék eltérése normális eloszlású véletlen változó a várható értéke nem haladja meg háromszor a szórást.
A központi határeloszlás tétel.
A centrális határeloszlás-tétel az elmélet csoportok szentelt létrehozó körülményeket, amelyek között van egy normális eloszlás. Ezek között tételek fontos helyet tartozik Ljapunov-tétel.
Ha az X valószínűségi változó összege számos kölcsönösen - független valószínűségi változók, azaz a hatását, amelyek mindegyike a teljes összeg elhanyagolható, akkor a valószínűségi változók eloszlása van a végtelenségig közelít a normális eloszlás.
A kezdeti és a központi pillanatok folytonos valószínűségi változó, ferdeség és csúcsossága. Mód és medián.
Az alkalmazott problémák, mint például a több száz matematikai tistike, az elméleti tanulmány empirikus eloszlás részlegeik, eltér a normális eloszlás, a WHO-felmerül az igény mennyiségi becslések ezeket a különbségeket. Erre a célra, mi vezetett különleges dimenzió jellemzőit.
Opredelenie.Moda folytonos valószínűségi változó (Mo (X)) - ez a legvalószínűbb érték, amelyre a valószínűsége pi vagy valószínűség-sűrűség f (x) maximumot ér el.
Opredelenie.Mediana folyamatos véletlenszerű velichinyX (Me (X)) - ez az értéke, amely megfelel a következő egyenletet:
P (X
Geometriailag egy függőleges vonalat X = Me a (X) osztja a görbe alatti terület alakja két egyenlő részre.
X pontban = Me (X), a F eloszlásfüggvény (Me (X)) =
Find Mo mód, a medián Me és M matematikai elvárás egy véletlen X változó a valószínűség-sűrűség az f (x) = 3x 2. ha X i [0; 1].
A valószínűség-sűrűség f (x) van maximuma az x = 1, azaz a f (1) = 3, tehát, Mo (X) = 1, az [0; 1].
Ahhoz, hogy megtalálja a medián jelöli Me (X) = b.
Mivel Me (X) megfelel annak a feltételnek a P (X akkor P (-∞ 3. megjegyzés az eredő érték Mo (X), Me (X), M (X) a tengelyen Ox: Opredelenie.Asimmetriey elméleti eloszlás az arány a harmadik központi pillanata érdekében egy percet, hogy a kocka a szórás: Opredelenie.Ekstsessom elméleti eloszlást az úgynevezett on-érték határozza meg a következő egyenletet: ahol - a központi pont a negyedik rend. Normális eloszlás. Amikor eltérés, eltekintve a normális eloszlás aszimmetria pozitív, ha a „hosszú” és a laposabb része a eloszlási görbe jobbra a pont az abszcisszán megfelelő vezetőképes módban; ha ezt a részét a görbe balra, a divat, az aszimmetria negatív (1A., b).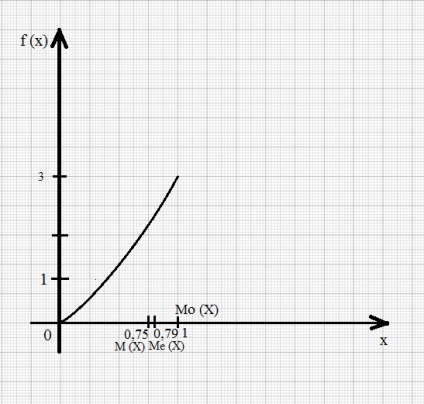

Csúcsosság jellemzi a „meredeksége” a görbe emelkedése az eloszlás a hasadási összehasonlítva a normál görbe, ha kurtosis polo-lakosok, a görbe egy magas és éles csúcs; esetén negatív kurtosis görbe hogy megfeleljen, és van egy alsó ferde tetején.
Belátható, hogy segítségével az összehasonlítás az említett referencia jellemzői hasonlóak feltételezéseket értékek matematikai elvárás és dis-persa normál és elméleti eloszlások.
Példa. Legyen egy diszkrét X valószínűségi változó adott eloszlás jog:
Keresés: ferdesége és csúcsossága az elméleti eloszlás.
Először megtalálják a várakozás SLE-véletlen változó:
Ezután kiszámítjuk a kezdeti és a központi pillanatok 2, 3 és 4-ed rendű, és a standard eltérés:
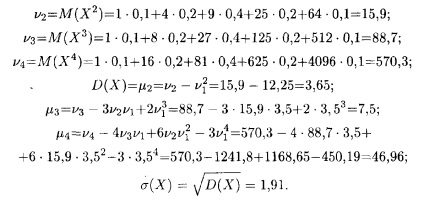
Most azt látjuk, képletek a szükséges ólom-fokozat:
Ebben az esetben a „hossz” az eloszlási görbe a verseny terített a jogot, a divat, a görbe önmagában nem-sokkal csúcsos, mint a normál görbe ugyanazokat az értékeket a matematikai várható értéke és szórása.
Tétel. Egy tetszőleges X valószínűségi változó, és bármilyen számú
Ԑ> 0 a egyenlőtlenségeket:
- a valószínűsége, hogy a szemközti egyenlőtlenség.
Legyen X -Expenses vizet, a haszonállatok (n).
A hipotézis, M (X) = 1000.
Ez nem kevesebb, mint 0,96.
A binomiális eloszlás Csebisev egyenlőtlenség formáját ölti: