Átalakítás puzzle Admiral Makarov (d

Ez az egység kapcsolódik a 6 négyzet rúd. A rudak barázdák, amelyek lehetővé teszik, keresztezésének bár a központban a csomópont. Az egyik a rudak nincsenek barázdák, akkor kerül az utolsó csomópont, és a szétszerelés során először eltávolítjuk.
Vesz egy ilyen rejtvényeket lehet például my-shop.ru
A különböző véres csomók
Mielőtt az a század elején, több száz éves fennállása játékok Kínában, Mongóliában és Indiában találták több mint száz változatait puzzle, konfigurációjában különböznek a bevágások a bárokban. De a legnépszerűbb két lehetőség van. Az 1. ábrán látható megoldódott nagyon könnyen, egyszerűen és azt. Ez a struktúra használják az ősi indiai koporsót. A rudak a 2. ábrán áll puzzle az úgynevezett „Ördög csomót”. Amint lehet képzelni, a neve megkapta a nehéz döntéseket.
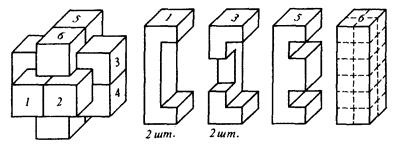
Ábra. 1. A legegyszerűbb változata „véres node” kirakós
Európában, ahol, mert a múlt század végén, a „Ördög Knot” már egyre népszerűbb, rajongók kezdtek gondolkodni, és nem állítja bár különböző konfigurációk kivágások. Az egyik legsikeresebb kit állít 159 rejtvények és áll 20 bar 18 faj. Míg az összes csomópont külleme nem különböztethető meg, ezek egészen másképp belsejében elrendezett.
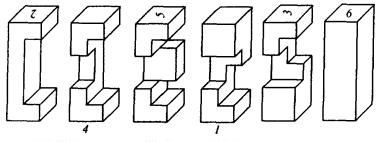
Ábra. 2 "Golovlomka Admiral Makarov"
Kitartóan minden ebben a keresést egy holland matematika professzora Van De Boer, aki saját kezével készített egy gyűjtemény több száz bar és összeállított táblázatok hogyan kell összeállítani a 2906 lehetőségek csomópontokat.
Ez volt a 60-as, 1978-ban az amerikai matematikus Bill Cutler írt egy programot a számítógép, és a nyers erő határozza meg, hogy van 119.979 lehetőségek rejtvények 6 elem, különböző kombinációi kiemelkedések és bemélyedések a bárokban, valamint az elhelyezés rúd, azzal a megkötéssel, hogy nem üregek belsejében a csomópont.
A meglepően nagy számú ilyen kis játék! Ezért, hogy megoldja a problémát, és szükség van egy számítógépre.
Mivel a számítógép oldja meg a puzzle?
Persze, nem egy személy, de nem valamilyen mágikus módon. Számítógépes megoldja rejtvényeket (és más tárgyak) a program, a programozók programokat írni. Írd meg, ahogy nekik megfelel, de úgy, hogy világos és számítógépek. Hogyan lehet egy számítógépes manipulálja a fa rudak?
Mi jár az a tény, hogy van egy sor 369 rudak, amelyek különböznek egymástól konfigurációi kiemelkedések (az első készlet azonosított Van De Boer). A számítógép kell adnia egy leírást a rudak. A minimális mélyedés (vagy a kiálló) a bárban - egy kocka éle 0,5 bar vastagságú. Nevezzük egy kocka. Általában, az ilyen 24 rudat tartalmaz egy kocka (1. ábra). A számítógép minden mozogni kezd a „kis” tömb 6h2h2 = 24 számot. A bár bevágások meghatározott szekvenciát a 0 és 1 a „kis” tömb: 0 felel vájt kocka, 1 - egész. Mind a „kis” tömbök saját számát (1-369). Ezek közül bármelyik lehet rendelni egy másik számot 1-6, megfelelő helyzetben a rúd belsejében puzzle.
Most viszont, hogy a kirakós. Képzeljük el, hogy az belefér egy kocka mérési 8h8h8. Ebben a számítógépes kocka felel meg „nagy” tömb álló sejtek 8h8h8 = 512-számok. Tegyél egy kis sáv belsejében a kocka - ez azt jelenti, hogy töltse ki a megfelelő mobil „nagy” tömb számok számával megegyező a bárban.
Összehasonlítva 6 „kis” tömbök és egyszerű, a számítógép (azaz. E. Program), mivel egészíti ki együtt a 6 bar. Az eredmények szerint a számok hozzáadását ez határozza meg, hogy mennyi és milyen „üres”, „tele” és a „túlzsúfolt” képződő sejtek fő tömb. „Üres” cella felel meg az üres tér belsejében a puzzle, „tele” - megfelel a kiemelkedések a bárokban, és a „zsúfolt” - kísérlet összevesd két egyszemélyes kocka, ami természetesen tilos. Egy ilyen összehasonlítást végzünk többször, nem csak a különböző bárokban, hanem tekintettel azok fordulat, a helyeket foglalnak el a „kereszt”, és így tovább. N.
Ennek eredményeként választják ki azokat a lehetőségeket, amelyek nem üresek és túlzsúfolt sejteket. A probléma megoldására lenne elég „nagy” tömbméret 6h6h6 sejteket. Kiderült azonban, hogy vannak olyan kombinációk bárok, teljesen kitöltve a belső térfogata a puzzle, de nem szedhető szét. Ezért a program képesnek kell lennie arra, hogy ellenőrizze a csomópont lehetőségét szétszerelés. Ebből a célból, Cutler és felvette egy tömb 8h8h8, bár a méret nem lehet elegendő ahhoz, hogy teszteljék minden esetben.
Ő tele van részleteket a variáns rejtvényeket. Belül a tömb program megpróbálja „mozog” a bárokban, t. E. mozgatja a „nagy” tömb méretét a bárban 2h2h6 sejteket. Displacement történik egy sejtet mind a 6 párhuzamos irányban tengelyei a puzzle. Az eredmények a hat kísérlet, amely nem alakul „zsúfolt” sejtek vannak tárolva, mint a kiindulási helyzetbe a következő hatos kísérleteket. Az eredmény fa gyártani az összes lehetséges mozgások, amíg minden blokk nem teljesen ki a váza vagy miután minden kísérlet, hogy továbbra is „túlzsúfolt” sejtek, ez volt az egyik, hogy nem lehet szétszerelni.
Ami kaptuk számítógép 119 979 változat a „Ördög Knot”, beleértve a nem 108, mint a régiek, és a 6402 verzió 1 egész nélkül vágások bar.
Vegye figyelembe, hogy Cutler feladta az általános probléma - ha a csomópont tartalmaz mind a belső üregek. Ebben az esetben a csomópontok száma 6 bar jelentősen nőtt, és a teljes keresési megtalálásához szükséges megvalósítható megoldásokat, nem reális, még a modern számítógépes. De mint látni fogjuk őt, a legérdekesebb és kihívást jelentő rejtvényeket találta az általános esetben - szétszedése puzzle, akkor lehet, hogy egy távol triviális.
Mivel a pórusok jelenléte, lehetséges, hogy egymás után mozgatni néhány rúd előtt képes lesz teljes mértékben elválasztani minden bárban. Mozgó bár elválik néhány bár ez megengedi a mozgás a következő sáv, és ezzel egyidejűleg bevonja a másik rúd.
Minél többet kell tennie manipulációk szétszerelés közben, annál érdekesebb és nehezebb változata a puzzle. A nyílások a bárokban úgy vannak elrendezve, ravaszul, hogy a megoldások keresése emlékeztet vándor a sötét labirintusban, ahol minden alkalommal jön valami ellen a falra, majd zsákutcák. Ez a fajta csomópont kétségtelenül megérdemel egy új nevet; fogjuk nevezni „SuperNode”. Szupercsomópontok komplexitás intézkedés hívják a mozgások számát az egyes rudak amelyet meg kell tenni, mielőtt az első elem elkülönül a puzzle.
oldat szupercsomópontok
A rajzok ilyen nehéz rejtvényeket szupercsomópontok, és nem arra, hogy felfedje titkait lenne túl kegyetlen, hogy még az ínyencek a rejtvényeket. Adunk egy határozatot szupercsomópontok egy kompakt, téglalap alakú.
Szétszerelése előtt take puzzle orientálódni, hogy az megfeleljen a rajz része szám 1. szétszerelés szekvencia van rögzítve, amely ötvözi a számokat és betűket. Számok jelentik a vonalak száma, betűk - mozgás iránya összhangban, hogy látható 3. és 4. ábrán, a koordináta-rendszer. Fölötti mozgás negatív irányban a koordináta tengely. Egy lépés - a mozgató 1/2 a szélessége. Ha a sáv mozgatni két lépést egyszerre, a mozgása van írva zárójelben a kitevő 2. Amikor mozgatni több részre, amelyek összekapcsolódnak egymással, arra a következtetésre jutnak számok n zárójelben, például (1, 3, 6) x. Válás bár a puzzle jelöli függőleges nyíl.
Most, hogy a bevált szupercsomópontok.
Puzzle W. Cutler ( "tüskés Bill")
Ez áll a részei 1, 2, 3, 4, 5, 6, amint a 3. ábrán látható is adott megoldási algoritmus. Érdekes, hogy a magazin «Scientific American» (1985 10-es szám) egy másik változata a puzzle, és azt jelentette, hogy a „tüskés Bill” egyedülálló megoldás. A különbség a kiviteli alakoknál - csak egy sáv: 2 és 2 részlet a 3. ábrán.
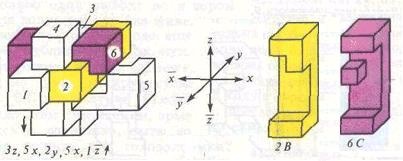
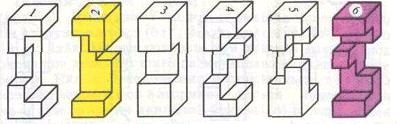
Ábra. 3 „Barb Bill” tervezte egy számítógép.
Tekintettel arra, hogy a 2. rész tartalmaz kevesebb vágást, mint a 2 munkadarab, helyezze be a „tüskés Bill” a fenti 3. ábrán az algoritmus sikertelen. Lehetne azt feltételezik, hogy a puzzle a «Scientific American» fog valamilyen más módon.
Filippa Dyubua puzzle (ábra. 4)
Ez megoldható a 7 mozog az alábbi algoritmus: (6 z) ^ 2, 3 x. 1 z. 4x, 2x, 2y, 2z. Ha ábrán az alkatrészek elhelyezkedését a B kanca szétszerelés. Ebből kiindulva a helyre, majd fordított sorrendben az algoritmus és a változás a mozgás irányát az ellenkező, akkor a kirakós.
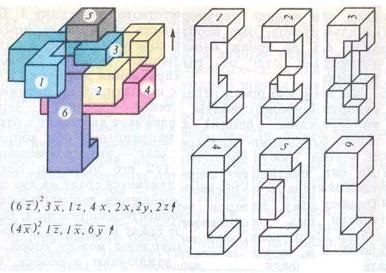
Ábra. 4 SuperNode F. Dyubaya összetettsége 7
Három szupercsomópontok D. Vakarelova.
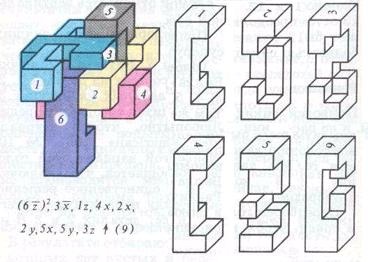
Ábra. 5 SuperNode 9 D.Vakarelova
Az első az ő rejtvények (5. ábra) - ez egy továbbfejlesztett változata a puzzle Dubois, azt nehezen 9. Ez szupercsomópont, mint mások, mint egy labirintus, mint amikor bontási felmerülő hamis mozog Izgalmas holtpontok. Egy példa egy ilyen holtpont - x W mozog. Z1 elején a szétszerelés. A helyes megoldás:
(6 z) ^ 2, W, X, 1Z, 4x, 2x, 2y, 5x, 5Y, 3Z?.
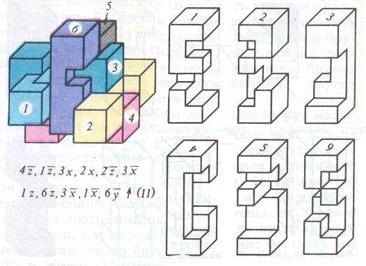
Ábra. 6 SuperNode D. Vakarelova 11
A második puzzle Vakarelova D. (. 6. ábra) van megoldva a következő képlet:
4 Z, 1 z. Sx, 2, 2 z. W. 1Z, 6Z, Z x. 1 x, 3Z?
és bonyolultsága 11. Figyelemre méltó, hogy bár 3-án a harmadik lépés egy lépést Sx és hátsó (B x) visszaadja a hatodik sebesség; és 1 bar, a második lépésben mozog 1 z. 7 és teszi folyamán vissza löketet.
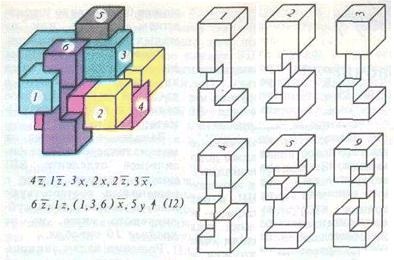
Ábra. 7 SuperNode D. Vakarelova 12
A harmadik puzzle (7. ábra) - az egyik legnehezebb. A megoldás:
4 z. 1 z. Sx, 2, 2 z. W. 6 z. 1z, (1,3,6) x. 5é?
míg a hetedik löket megismétli az előző puzzle, akkor menjen a 9. lép fel egy teljesen új helyzet: hirtelen az összes vonal mozgása megáll! És akkor meg kell, hogy azonnal kitalálni 3 bar (1, 3, 6), és ha ez a mozgás tekinthető 3 fordulat, akkor a komplexitás a puzzle lesz egyenlő 12.