alapvető meghatározások
A rendszer a közönséges differenciálegyenletek lehet az az alábbi általános formája:
Vagy vektor formában:
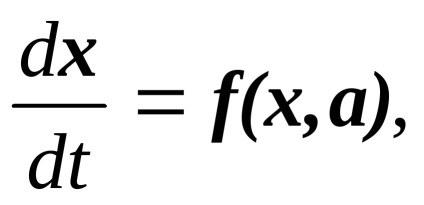
A rendszer megoldás a funkciók, amelyek megfelelnek az eredeti egyenletnek. A megoldás is írva vektorba egyenletek formeSistema
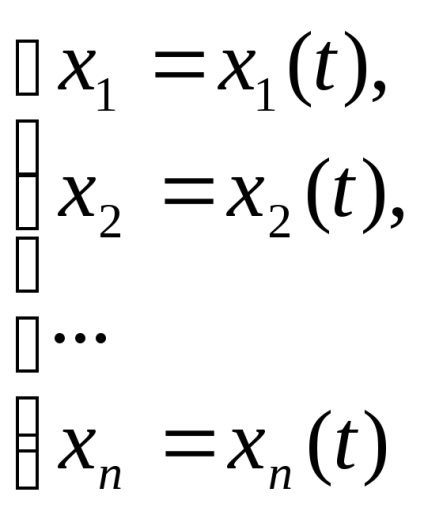
Ez egy paraméteres görbe egyenlet n-dimenziós térben a valós tengelyek. Ez a görbe nazyvayutfazovoy pályája a rendszer differenciálegyenletek. Abban az esetben, i = 1,2,3 röppálya ad egy vizuális ábrázolás a viselkedését a megfelelő megoldások (ábra. 3.2).
Ris.3.2.Resheniya és fázis pályáját másodrendű rendszer
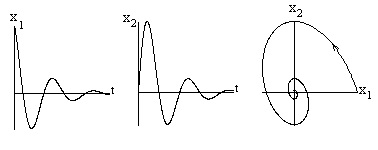
A készlet az összes rendszer a fázis pályák képezi vfazovy portré a rendszer. Így prostranstvonazyvayutfazovym űrrendszereket. Így, a fázis térben megfelelnek a készlet minden lehetséges állapot a dinamikus rendszer. Minden új rendszer állapotát felelnek meg a különböző pontokat a fázis helyet.
Megoldás a differenciálegyenlet-rendszert határozza meg az evolúció a tanulmány a dinamikus rendszer időben. Ez a fejlődés képviseli a mozgás a fázis pont a megfelelő pálya. rendszer állapot momentt nem csak attól függ, hogy az idő, hanem a kezdeti állapot, amelyben a rendszer található, abban az időben. Ez utóbbi kapcsán nazyvaetsyanachalnym állapot megoldására a rendszert.
Lehetséges út, amely csak egy pont: ez egy pont a többi ilistatsionarnye pontot. többi pontot az jellemzi, hogy az idő származékai változók ezeken a helyeken nulla. Ahhoz tochkabyla többi pont, szükséges és elégséges ahhoz, hogy a feltételeket.
Ha a pálya kétszer halad át ugyanazon a ponton, ez zárt pályán, amely az úgynevezett ciklust. és a megfelelő megoldás lesz periodikus.
Így vannak háromféle utak. lezáratlan, zárt (ciklus) itochki pihenni. Minden pont a fázis tér tulajdonában van pontosan egy utat. Ezért, ha a két fázis pályákat egy közös pont. akkor egybeesnek.
Megjegyezzük továbbá, hogy a rendszer típusának
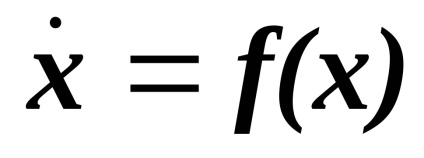
Építése fázis portrék
Térjünk vissza a modell a mechanikai rendszert példában leírt módon a 3.1. Az egyenlet egy nemlineáris modell
.
A másodrendű egyenlet mehet az autonóm rendszer az űrlap
,
Ha most a rendszer, hogy megszüntesse az idő t. Megkapjuk a differenciálegyenlet-rendszer a fázis síkban pályáira
átírhatjuk az utolsó egyenlet az alábbiak szerint:
Ezután feltéve, hogy akkor, és integrálása után az egyenlet belül otdopoluchaem egyenlőség
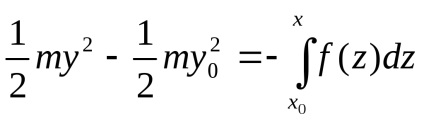
amely lehet újraírni az alábbiak szerint:
Vegyük észre, hogy van egy képlet mozgási energia egy dinamikus rendszer, és a
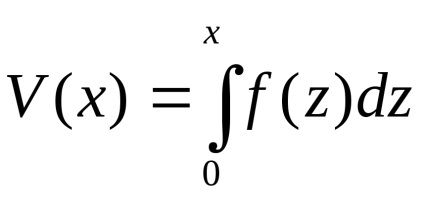
- formula a benne rejlő energiát. Így az egyenlet fejezi ki a törvény az energiamegmaradás:
valahol az összes energia a rendszer.
Nyilvánvaló, hogy ez az egyenlet - az egyenlet a fázis pályáira nemlineáris konzervatív rendszer, hiszen integrálásával kaptunk egyenlet
Így, különböző értékeket a fázis E síkban megfelelnek a különböző görbék állandó energiájú. Helyhez pontok a rendszer azok a pontok, M * (x *, 0). gdex * - gyökereit. Ebben az esetben, ha az átírási a törvény az energiamegmaradás formájában
,
könnyen lehet fázisban pályákat.
Vezetett általános szempontok lehetővé teszik, hogy vizsgálja meg a mozgásegyenletek az inga a környezetben ellenállás nélkül, amely a forma
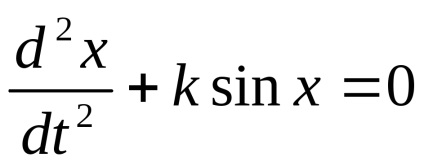
Mivel az egyenlet egy speciális esete az egyenlet, azt lehet értelmezni, mint a leíró egyenletet lineáris mozgás az egység testtömeg súrlódás nélkül az intézkedés alapján nemlineáris rugó, ahol a visszaállító erőt egyenlő. Ebben az esetben, az önálló rendszer, amely megfelel az egyenlet, írott formában
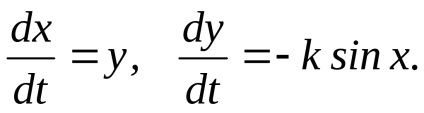
Egyes pontokat itt lesz differenciálegyenlet-rendszert fázis pályáira formájában fog
Elválasztása a változók végső egyenlet és integrálása, megkapjuk az egyenlet a fázis pályáira
Az utolsó egyenlet egy speciális esete a törvény az energiamegmaradás, ahol a potenciális energia adja
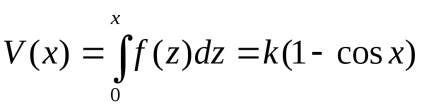
Meghatározása után az érték, akkor felvázolni egy vázlatos képet a viselkedését a pályákat a fázis síkban, ha használjuk az arány.
Az így kapott fázist portré mutatja (ábra. 3.3), hogy ha otdo energia változik, a megfelelő fázisra pályák vannak zárva és az egyenletnek periodikus megoldásokat. Másrészt, ha a megfelelő fázisban pályákat nem zárt, és az egyenletnek periodikus megoldásokat. Érték felesége fázis sík az fázis röppálya, amely elválasztja egymástól a két különböző típusú mozgás, mint nazyvayutseparatrisoy pályáját. Hullámos fázisú pályákat kívül fekszik szeparatrixokkal megfelelnek a forgómozgásának egy inga, és zárt pályákon található körülhatárolt területen szeparatrixokkal - a rezgőmozgás.
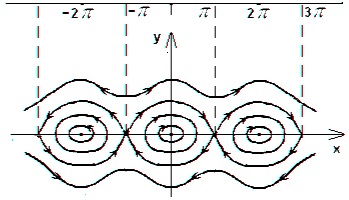
Ábra. 3.3. A fázis portré a nemlineáris konzervatív rendszer
A 3.3 ábra látható, hogy a szomszédságában a fixpontok gdepovedenie fázist pályákra eltér a fázis viselkedését a pályák a szomszédságában a fixpontok, ahol
Nézzük, mi befolyásolja a viselkedését a fázis pályáira a konzervatív rendszer lineáris súrlódás. Ebben az esetben az egyenlet
Ábra. 3.4.Fazovye portrék konzervatív rendszerek súrlódás
Melyik rendszer egy nem konzervatív. Ha a súrlódás elég kicsi ahhoz, vagyis lehetséges rezgések az inga képest az egyensúlyi helyzet, ki lehet mutatni, hogy a fázis trajektóriák amint azt vázlatosan a 3.4 ábra, a. Ha a súrlódási megakadályozza az esetleges rezgés az inga képest az egyensúlyi helyzet, a minta a fázis pályák lesz a ábrán bemutatott formában. 3,4, b.
Ha most összehasonlítjuk a fázis portré egy konzervatív rendszer utolsó két fázisban portréi nem konzervatív rendszerek, akkor látható, hogy a zárt szakasz pályáját az alacsony súrlódású, beköltözött egy spirál, és egy erős súrlódás - az utat, amely része a szinguláris pontok bizonyos irányban.
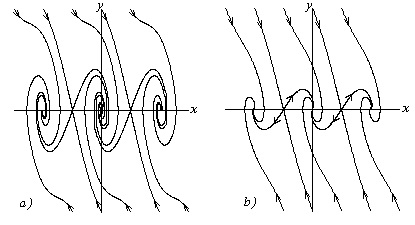
Ábra. 3.4.Fazovye portréi rendszerek súrlódási:
a- kis súrlódású; b- nagy súrlódási