Abszolút és relatív hiba
Elemei az elmélet hibák
Pontos és közelítő száma
Pontossága általában nem kétséges, amikor integer értékeket az adatok (2 ceruza 100 fák). Azonban a legtöbb esetben, amikor a pontos szám értékét nem lehet megadni (például a tárgy a mérés, megszüntetve az eredmények a műszer, stb), van dolgunk hozzávetőleges adatokat.
Hozzávetőleges érték szám némileg eltér a pontos értéket, és lecseréli a számítások során. A mértéke a közelítő értékek különbségek annak pontos értékét jellemzi egy hiba.
Vannak az alábbi fő hibaforrás:
1. hibák készítmény a probléma. felmerülő eredményeként közelítő leírását valós jelenségek szempontjából matematika.
2. módszer hibáiról. hozzák azt a nehézséget, vagy képtelen megoldani a problémát, és helyette egy hasonló, mint, hogy lehetséges alkalmazni egy jól ismert és hozzáférhető módszer megoldások és az eredmény közel a cél.
3. Súlyos hiba. kapcsolatos közelítő értékeit a bemenő adatok és az eredmény a fenti számítások hozzávetőleges számokat.
4. kerekítési hiba. értékeket társított kerekítési bemeneti adatokat, közbenső és végső eredmények, alkalmazásával kapott a számítási eszközöket.
Abszolút és relatív hiba
Könyvelési hibák fontos szempont alkalmazásának numerikus módszerek, mert a hiba a végeredmény a megoldás az egész probléma a termék az interakció mindenféle hibákat. Ezért az egyik fő célkitűzése az elmélet hibák a becslési eredmény pontossága alapján a pontossága a bemeneti adatokat.
Ha - a pontos számot, és - annak közelítő értékét, hiba (hiba) közelítő érték a mértéke közelségét annak értékét a pontos értéket.
Egy egyszerű kvantitatív hiba az abszolút hiba, amely a meghatározás szerint
Amint látható képletű 1.1.2-1, az abszolút hiba ugyanaz egységek, mint az értéket. Ezért a legnagyobb abszolút hiba nem mindig lehetséges, hogy a helyes következtetést a minősége a közelítés. Például, ha. de beszélünk a részleteket a gép, a mérések nagyon durva, és ha a méret a hajó, - nagyon precíz. Ebben a tekintetben, a fogalma relatív hiba, amelyben az abszolút értéke a hiba összefügg a modulusa közelítő értékek ().
A relatív hibák kényelmes, különösen, hogy nem függ az értékek a skála és a mérési adatok egység. A relatív hiba mérjük, mint egy frakciót vagy százalékos. Például, ha a
,a. Aztán, mintha,
Ahhoz, hogy számszerűen értékelni a funkció a hiba, meg kell tudni az alapvető szabályokat a számolás hibák Művelet:
· Az összeadás és kivonás számok abszolút hiba számok összeadódnak
· A szorzás és osztás számokkal egészül ki egymást a relatív hiba
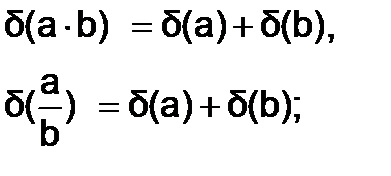
· A hatványozás hozzávetőleges számát a relatív hiba szorozva a kitevő
Példa 1.1.2-1. Dana funkció :. Keresse az abszolút és relatív nagysága a hiba (az eredményeképpen az aritmetikai műveletek), ha az értékek ismertek, és 1 - a pontos számot, a hiba nulla.
Meghatározásával így, a relatív hiba, lehet találni egy abszolút hibaértéket mint ahol az érték határozza meg a közelítő értékek
Mivel a pontos érték általában nem ismertek, a számítási képleteket, és nem lehet a fent felsorolt. Ezért a gyakorlatban, értékelje a hibahatár típusok:
ahol - ismert értékek, amelyek a felső határa az abszolút és relatív hiba, különben ők nevezik - a korlátot, és korlátozza a relatív hiba. Így, az aktuális érték tartományok:
Ha az érték nem ismert, akkor. és ha az érték nem ismert. az
Korlátozása abszolút hiba típusának függvényében. differentsiruemoyv előre meghatározott területen, az ismert értékek az érveket. és ismert abszolút hibahatár érveket. a következőképpen számítjuk ki:
és ennek megfelelően a maximális relatív hibafüggvényt
Abban a különleges esetben, a függvény egy változó (ha m = 1):
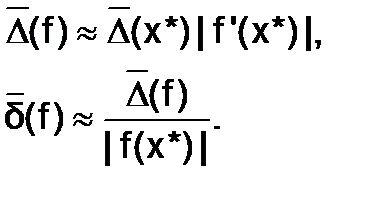
Primer1.1.2-2 .Otsenit abszolút és relatív hiba a hozzávetőleges száma.
Száma - egy transzcendens szám, ez a végtelen nem periodikus frakció.
Közelítő értéket a számot.
A határ az abszolút hiba. a relatív hiba