A vizuálisan érdekes!
Sokféleséget.
Izomorf gráfok.
Megjegyezzük, hogy a G gráf (ábra. 1) is képviseli különböző módon.
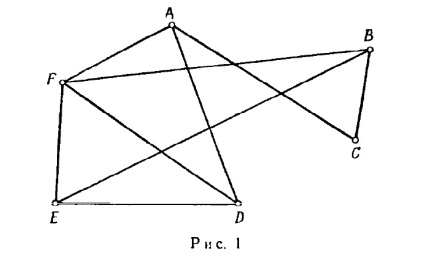
Először is, nem szükséges, hogy képviselje a szélei egyenes. Mi lehet elvégezni minden összekötő vonalak azonos csúcsok, mint korábban. Például, egy grafikon G reprezentálható ábrán látható módon. 7.
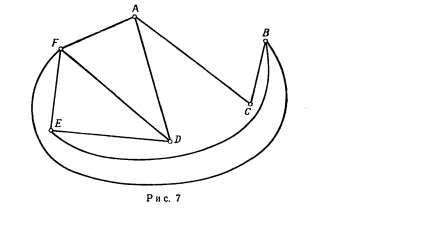
Másodszor, önkényesen tetejére helyezzük a gépet. Például, csúcsai G lehet elhelyezve, ábrán látható. 8.
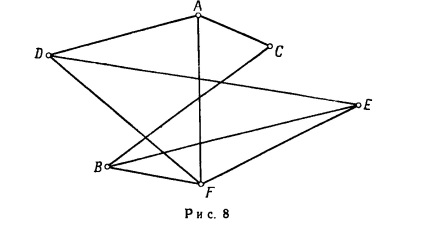
Ha figyelembe vesszük a három grafikonok ábrán látható. 1., 7. és 8. a grafikonok leíró során a sportesemény, akkor pontosan tartalmazza ugyanazt az információt, hogy milyen csapat játszott egymással; abban az értelemben, hogy ez ugyanaz a grafikonon. Megbeszéljük. Két grafa- jelöli a G1 és G2 - izomorfak, ha azok megfelelnek az ugyanazon a listán játékokat játszott. Más szóval, ha a grafikonok G1 és G2 izomorf. ugyanaz a csúcsok számát és bármely két a gráf G1, mondjuk B1 és C1, vannak összekötve egy él megfelelő csúcsait B2 és C2 grafikon G2 is össze van kötve egy él, és vissza.
E meghatározás szerint, a három grafikonok látható. 1., 7. és 8. izomorf (azaz. E. szerkezete ugyanaz), annak ellenére, hogy máshogy néznek ki.
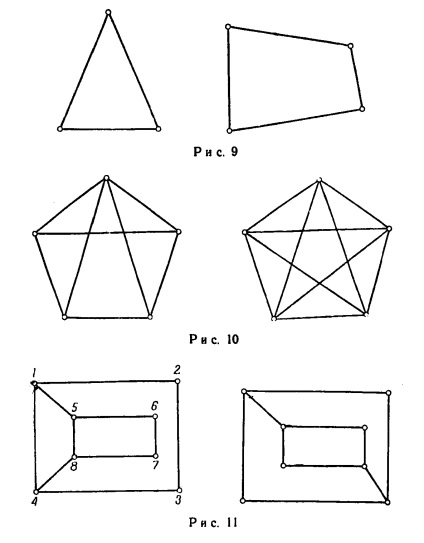
Gyakran kell döntenie, hogy az a kérdés, hogy a két adat izomorf gráf. Néha azonnal világos, hogy ez nem így van. Például, a grafikonok ábrán látható. 9, nem lehet izomorf, mert a csomópontok száma más. Lehet, hogy nem izomorf és grafikonok ábrán. 10, mivel ezek nem egyenlő számú élek.
Annak érdekében azonban, hogy azt mutatják, hogy nem izomorf a grafikonok ábrán látható. 11 szükséges néhány finomabb érv. Így látható, hogy az első oszlop egy olyan szekvenciát nyolc szomszédos élei (vagyis az élek páronként, amelyeknek egy közös vertex ..): (1,2), (2,3), (3,4), (4,8 ), (8,7), (7,6), (6,5), (5,1), az visszatér kiindulási vertex, mivel nincs ilyen szekvenciát a második oszlopban. Szóval, nem számít, hogyan jelöljük a csúcsai a második grafikon, nem tudunk minden pontpár él köt össze a grafikonon szereplő második megfelelő pontpár él köt össze is.
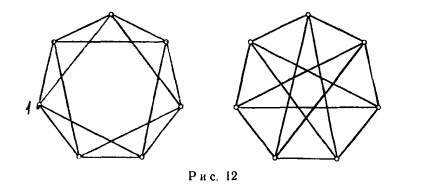
Ha csak nem látni, hogyan kell bizonyítani, hogy a két görbe nem izomorf, akkor az a kérdés, hogy izomorfizmus is meglehetősen nehéz. Példaként, úgy a két grafikon ábrán látható. 12; Ezek a diagramok valóban izomorfak.