A több szabadsági fokkal

Home | Rólunk | visszacsatolás
Az első részben a kiadvány hat előadások közzététele fizikai értelmében az alapvető fogalmak és a mechanika törvényeit.
A második része a folyamatos előadássorozatot fizika és tartalmaz kilenc előadást molekuláris fizika és a termodinamika.
A tanulmány tárgyát molekuláris fizika mozgása nagy gyűjtemények molekulák. A tanulmány statisztikai ég és termodinamikai módszerekkel.
Molekuláris fizika származik a koncepció az anyag molekuláris szerkezetére. Mivel a részecskék száma a macrosystem nagy Zuko vney-dimenziós, statisztikus, azaz valószínűségi jellegű. Alapján bizonyos modellek molekuláris fizika lehetővé teszi obyas menet megfigyelhető tulajdonságok nagyrendszerek (álló rendszerek igen nagy számú részecske), amíg a kumulatív hatása egyes intézkedések mo-molekulák. Ez használ egy statisztikai módszer, ahol mi integrál-akció resuyut nem különálló molekulák és az átlagértékeket egyes változók.
A használat során a koncepció a termodinamika és fizikai mennyiségeket-hordozó rendszer általánosságban, például térfogat, nyomás és hőmérséklet. Termodinamika közös elveken alapuló, vagy az elvek, amelyek általánosítása kísérleti tényeket.
Termodinamikai és statisztikai módszerek tanulmányozására makrosis-kiegészítő. Termodinamikai módszer lehetővé teszi számunkra, hogy tanulmányozza a jelenséget tudta nélkül a belső mechanizmusokat. A statisztikai módszer lehetővé teszi, hogy megértsük a jelenséget hoz létre kommunikációt viselkedését a teljes rendszer viselkedését és jellemzőit az egyes részecskék.
FIGYELEM! A javasolt kiadvány megkönnyíti a munkát a diákok, de nem helyettesíti MAGAD előadást a közönség!
Molekuláris-kinetikai elmélet (ICB)
1. A koncepció az ideális gáz. Molekuláris kinetikus értelmezése hőmérsékletet. Makroszkopikus paramétereinek a rendszert.
2. A több szabadsági fokkal. ekvipartició energia törvény. A belső energia az ideális gáz.
3. A gáz nyomása a szempontból a molekuláris kinetikai elmélet ideális gáz (alapegyenletének molekuláris kinetikai elmélet).
4. Az állapotegyenlet az ideális gáz (Mengyelejev-Clapeyron egyenlet).
A koncepció az ideális gáz.
Úgynevezett ideális gázok, közötti kölcsönhatás molekulák elhanyagolható, és az állam, melynek leírása a Clapeyron-Mendeleev.
A modell ideális gáz.
1. Nettó térfogata gázmolekulák elhanyagolható térfogatához viszonyítva az edény.
2. között a gázmolekulák offline interakciót erők.
3. Az ütközések gázmolekulák egymással és egyáltalán rugalmas érfalat.
Kölcsönhatása molekulák bármely gáz válik elhanyagolhatóan gyenge alacsony gázok sűrűsége. nagyvákuumban. Gázok, például levegő, nitrogén, oxigén, még normál körülmények között, azaz a szobahőmérsékleten és atmoszferikus nyomáson kis mértékben eltér az ideális gázokra. Különösen közel az ideális gáz hélium és hidrogén.
Ne gondoljuk, hogy a kölcsönhatás a molekulák az ideális gáz létezik. Éppen ellenkezőleg, a molekulái egymással ütköznek, és az ütközések elengedhetetlen a létesítmény egyes termikus tulajdonságainak a gázt. De ütközések annyira ritka. a legtöbb időt a molekulák mozognak, mint szabad részecskék.
Ez volt az ütközés molekulák között lehetővé teszi, hogy adjon meg egy paraméter a hőmérséklet. Testhőmérséklet jellemzi az energia, amellyel a molekulái mozognak. Egy ideális gázt egyensúlyi körülmények között, az abszolút hőmérséklet arányos az átlagos energia a transzlációs mozgás a molekulák.
Definíció. Úgynevezett makroszkopikus rendszer, amelyet egy hatalmas számú részecske (molekulák, atomok). A jellemző paraméterek a rendszer viselkedését (például gáz) egésze nevezik makroparamétert. Például, a nyomás P. V térfogat és T hőmérséklet a gáz - makroparamétert.
A jellemző paraméterek viselkedését az egyes molekulák (sebesség, tömeg, stb) nevezzük mikroparamétert.
A több szabadsági fokkal.
Opredelenie.Chislom szabadsági fokú mechanikai rendszer a független változók száma. amellyel meg lehet adott pozícióban a rendszer az űrben.
a) Mivel a térbeli helyzetét az anyag pont teljesen határozza meg három koordinátáját (például Descartes x, y, z vagy gömb. vagyis azt a számot a szabadsági fokok i = 3).
b) A rendszer 2 mereven kapcsolódó tömege pontot (a szegmens őket összekötő rögzített). Koordinátáit a 2 pont összefügg. ahol 5 elegendő, hogy meghatározza a koordinátákat, és a hatodik megtalálható a fenti kapcsolatok, azaz i = 5. Ha a pontok nincsenek mereven összekapcsolva, a szám a szabadsági fokok i = 6. A változás ad egy bizonyos fokú szabadságot, amely az úgynevezett oszcilláló.
Szabályozási rendszer, amely 2 mereven kapcsolódó anyagot pontokat (vagy például, egy rúd) lehet beállítani az alábbiak szerint: 3 beállított koordináta-rendszer tehetetlensége és a központ C 2 a szög, amely meghatározza az irányt a rendszer tengelye a térben (7.1 ábra.).
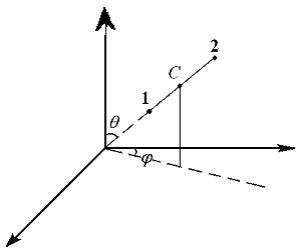
Az első három szabadsági fokkal hívják transzlációs. míg a másik kettő - forgási. Rotációs szabadsági fok megfelelnek körüli forgatás a 2 egymásra merőleges tengely (i = 5). c) rendelkezni teljesen merev test lehet meghatározni a koordináták megadásával a tömegközéppontja 3 (transzlációs szabadsági fok) és 3 szög (rotációs szabadsági fok). T.e.i = 6
A törvény ekvipartició energia
A klasszikus fizika, statikus kijelzők Boltzmann törvény egységes energia eloszlását szabadsági fokú molekulák: az egyes szabadsági foka a molekulák átlagos azonos mozgási energia, ravnayakT. Meg kell jegyezni, hogy a transzlációs és rotációs mozgások jár csak a mozgási energia, míg a oszciilálómozgás jelenléte miatt, és a kinetikus és potenciális energiájának. ráadásul az átlagos értéke a potenciális és kinetikus energia ugyanaz. Ezért minden egyes rezgési szabadsági foka átlagosan két feléből kT. Az átlagos energia a molekula egyenlőnek kell lennie:
ahol (Boltzmann állandó); Itt - az összege transzlációs, rotációs száma és kétszer annyi rezgési szabadsági fokkal a molekulák: