A szögsebesség és szöggyorsulása a test vektoriális mennyiség
A szögsebesség és szöggyorsulása a test vektoriális mennyiség
Bizonyítása tételei kinematikája és dinamikája, ha figyelembe vesszük a szögsebesség és a szöggyorsulás vektorként mennyiség lehet egyszerűsíteni. Vector (ábra. 49), mely a szögsebesség, épül a forgástengely, irányítja rá a tengely mentén a másik oldalra, hogy megkeressék a végéhez, hogy mi történik forgatni az óramutató járásával ellentétes. Indítsa el lehet helyezni bármely pontján a tengely, - egy csúszó vektor. modul | | = | Dφ / dt | = | | Ez megegyezik az abszolút értéke a szögsebesség.
E
Ha hogy az egység vektor z tengely -












A vektor egybeesnek az irányt, lehet, hogy más. Ha a forgatás gyorsulás, mindkét vektorral azonos irányban (ábra. 50), ha a lassú - különböző (51. ábra).
A fogalmak a vektor szögsebességgel és szöggyorsulással, akkor kifejezetten a lineáris sebesség és lineáris gyorsulási formájában vektor termékeket.
Az expressziós lineáris sebesség és a gyorsulás, mint vektoron
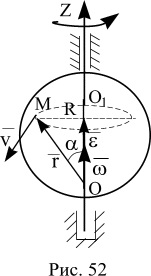
Tegyük fel, hogy van egy test körül forgó rögzített tengely. Ábrázolása a szögsebesség és szöggyorsulással vektorként. Az elején a rendek, hogy a pont a forgástengely. Vegyünk bármely pontján a test M. A pont a sugár vektor a pont M. A bezárt szög a Z tengely, és jelöljük α. Megmutatjuk, hogy a lineáris sebesség vektor M pontot.
Ez könnyen ellenőrizhető, emlékeztetve a meghatározása a kereszt termék két vektor. A kereszt terméket Két vektor egy új vektor merőleges a síkra, amelyben fekszenek a két adat vektor, és egyenlő a terméket modulo modulusok a szinusz a szög közöttük. A vektor (ábra. 52) síkjára merőleges, és ΔOMO1 ωr sin α = ωR (R = R sin α a ΔOMO1).
lineáris sebesség v vektor = ω R. R. és merőlegesen, azaz ΔOMO1 sík irányában forog, és az óramutató járásával ellentétes. Következésképpen, a vektorok és egyenlő, mint szükséges.
- az alap képletű kinematika vagy Euler-képlet.
az
Egy vektor összege két vektor. Megmutatjuk, hogy - ott āτ. - AN - vektorok az érintő és a normális gyorsulás. Vektor egyenlő modulo folyadékok Könnyû granulátumok Folyadékok sin α = folyadékok Könnyû granulátumok Folyadékok és merőleges a síkra, amelyben fekszenek mindkét, azaz a ΔOMO1 síkon. Ezért, egy vektor merőleges a sugara forgatás és szöggyorsulással egyenlő a termék által az elforgatás sugarának, azaz Ez a vektor āτ.
vektor modulo egyenlő ωv sin β, β = 90 Nr és ωv sin β = ωv = ω 2 R. mivel v = ω R.
Ő merőleges a síkra, amelyben hazugság, és ez sugárirányban a középpont felé (ábra. 53).
Példa. A szíjtárcsa sugara R = 0,5 m csavar törzs, a szabad vége, amely a felfüggesztett teher A (ábra. 54). A terhelés csökken egyenletesen gyorsuló nyugalmi gyorsítási aA = 2 m / s 2, és forgatja a szíjtárcsát. Keresse meg a törvény a forgómozgást a tárcsa, szögsebesség, szöggyorsulással bármikor t. valamint a sebesség és a gyorsulás Am M pont fekszik a tárcsa peremén. Grúzia halad egyenletes gyorsulás, így megtalálja a sebesség Va = AAT-= 2t m / s. terhelés sebesség egyenlő a sebesség pont a RIM, azaz vM = VA = 2t. majd ω = a VM / R = 4t c -1. szöggyorsulás ε = dω / dt = 4 c -1. azaz ε = const és a tárcsa forgása egyenletesen gyorsuló. ω0 = 0, ezért forgatás a törvény:
rendes fogaskerék
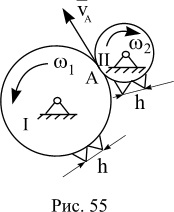
A forgó mozgás széles körben elterjedt a különböző gépek és mechanizmusok. A forgatás lehet továbbítani távolságon keresztül révén flexibilis csatlakozások (transzfer öv), vagy közvetlen érintkezés útján (súrlódásos vagy fogaskerekek). Az öv és frikciós áttételek használt súrlódási erő, és egy fogaskerék - mechanikai kapcsolódást. Minden ilyen típusú programok olyan vezető elem, amely tájékoztatja a mozgás, és a hajtott tag, amely nyert a mozgás a meghajtó tag. Vegyünk egy sorozat fogaskerék vagy vegyületek sorozatát fogaskerekek.
Vegyület fogaskerekek amelynek tengelyeket minden forgatni fix csapágyazású nevezett közönséges vegyület vagy egy közönséges fogaskerék (ábra. 55).
A távolság két szomszédos fogak nevezzük lépést fogaskerék h.
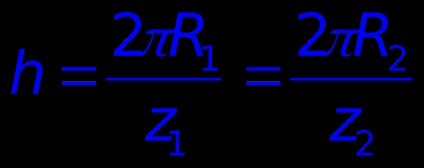
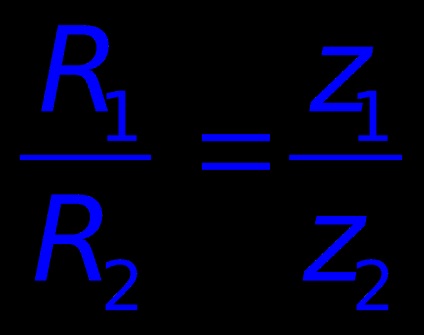
ahol R1. z1 - sugár és fogszáma kerék I; R2. z2 - sugár és fogszáma kerék II.
Rendes átviteli jellemzi a áttétel. I1,2 áttétel az áttétel megegyezik a szögsebesség ω1 a meghajtó kerék a hajtott szögsebesség ω2. i1,2 = ω1 / ω2.
Ha n hálószembőségű kerekek, a áttétel egy átviteli aránya eléri a termék a kapcsolt párok:
ahol m - száma a külső linkek.
Amikor egy belső fogazatú (. 56. ábra), a fogaskerék arány pozitív, míg a külső - hátrányosan.
Fogaskerék három fogaskerekek (ábra. 57). Az első kerék átmérője 0,2 m és teszi 7200 fordulat / perc. A második kerék - 4000 ford / perc, és a harmadik - 600 fordulat / perc. Határozza meg a átmérőjét a második és a harmadik kerék.
Nincs helyes válasz.
Kerék sugara 0,8 m, forgó állandó gyorsulás gyorsítás közben álló helyzetből, míg a lekötött 750 fordulat. Határozzuk földi időben, ha a sebesség pont a felni elért 200 m / s.
Kerék sugara 0,5 m, forgás közben egyenletesen gyorsuló, 10 van egy szögsebességet n = 120 fordulat / perc (N0 = 0). Határozza meg a gyorsulás a pontjában a kerékabroncs a t = 1 perc.
Fogantyú OA (ábra. 58) el van fordítva a törvény φ = 5t. Annak meghatározására, hogy mennyi ideig terhelés emelkedik a magassága 5 m, ha r1 = 0,2 m; R2 = 0,3 m; r3 = 0,15 m.
A forgó test egy rögzített tengely által meghatározott egyenlettel φ = 1,5t 2 - 4t. Határozza meg a sebesség és a gyorsulás a test egy bizonyos távolságban lévő pontig forgástengelye 0,2 m t1 időpontban = 2.
hallgató bontatlan oktatási formák az alábbi főbb lépéseket: samostoyatelnoeizuchenie fizikája uchebnymposobiyam. tverdogotela mozgása ahhoz képest, egy rögzített tengely. Ha I = const, akkor M = I, ahol - szöggyorsulása a szervezetben. 26.
hallgató bontatlan oktatási formák az alábbi főbb lépéseket: samostoyatelnoeizuchenie fizikája uchebnymposobiyam. tverdogotela mozgása ahhoz képest, egy rögzített tengely. Ha I = const, akkor M = I, ahol - szöggyorsulása a szervezetben. 26.
Tankönyv
- uchebnoeposobie. speciális didaktikai eszközök, hozzájárulva a hallgatók önálló munkáját a fejlődés a téma; bemutató - uchebnoeposobiedlyasamostoyatelnogoizucheniya.
Állami Oktatási szabvány
tanulmány. tverdogotela 1.2 2. téma: Dynamics of anyagi szempontból Dynamics egy anyagi pont és transzlációs mozgást tverdogotela. TVERDOGOTELAKinematika. Shahin EL Fizika: Uchebnoeposobiedlyasamostoyatelnoy munka hallgatói / 3rd ed.
tanulmány. tverdogotela 1.2 2. téma: Dynamics of anyagi szempontból Dynamics egy anyagi pont és transzlációs mozgást tverdogotela. TVERDOGOTELAKinematika. Shahin EL Fizika: Uchebnoeposobiedlyasamostoyatelnoy munka hallgatói / 3rd ed.