A szalagok azonos vastagságú és egyenlő dőlés
A szalagok azonos vastagságú
Tegyük fel, hogy van egy vékony lemez (film) formájában egy ék csúcsszöge egyenlő $ \ alpha \ $ (1. ábra). Ezen a lemezen esik monokróm hullám. Felismerték a felső és alsó felületei a film. Ezek a visszavert hullámok koherensek legyenek, ami azt jelenti, hogy amikor leadott képesek beavatkozás.
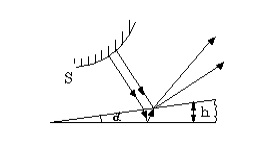
Sugarak, amelyek tükrözik a felső és az alsó lemez felület nem párhuzamos. Alakult a gerendák között útkülönb ($ \ háromszög $). Különböző pontjain az ék, akkor egy másik utat különbség. Meg lehet meghatározni:
ahol a $ h $ - rétegvastagság, $ N $ - törésmutatója a közeg, ahol a fénysugár.
Hagyja, hogy a sugarak esnek az ék szöge 90 $ ^ 0 $ a felszínre. Továbbá meg kell szem előtt tartani, hogy amikor egy hullám visszavert fény egy közepes nagy törésmutatójú elveszíti fél hullámhossz. Mivel a törésmutatója az ék nagyobb, mint a levegőé, a fény elveszti fele a hossza a reflexió a felső felületén az ék. Ebben az esetben az optikai út különbség, írunk ki:
Problémák kontroll minden tantárgyból. 10 éves tapasztalat! Ár 100 rubelt. 1-jétől nap!
Ebben a koordináta $ x $ társítható az arány a film vastagsága:
Koordinátái minimumok a beavatkozás megtalálható a tudatban, hogy:
Aztán, figyelembe véve (4), azt találjuk, $ x $:
Végén az ék, mi lesz a minimum. láthatjuk a fénycsík között min - max. Emellett egy ilyen fóliacsíkot vannak elrendezve egyenlő távolságra egymástól:
Csík ilyen látható a filmben is. A zenekar azonosnak kell lennie a rétegvastagság, innen a név „egyenlő vastagságú csíkokra.”
A sávok egyenlő lejtőn
A vékony lemez (film) egy sík párhuzamos (azonos vastagságú). Ezen film esnek sugarak különböző dőlésszöge (2. ábra). Ebben az esetben, az út különbség zavaró hullámok függ a beesési szögtől. Ennek megfelelően a beavatkozás minimumok és maximumok kövesse a szögek, amelyek a beeső sugarak. Megfigyelni az interferencia mintázat kell gyűjteni a visszavert sugarak párhuzamosan. Következésképpen a vizuális eszköz kell összpontosítani a végtelenbe. Ezért úgy gondoljuk, hogy a szalagok egyenlő hajlam figyelhető meg a végtelenben. Az interferencia a gyakorlatban a párhuzamos lemezek megfigyelt helyezve az utat a visszavert sugarak gyűjtőlencse. Ahol a képernyő a fókusz síkjában a lencse.
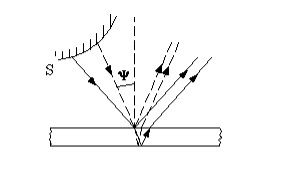
ahol $ \ vartheta $ - beesési szögének hullámok felső felületén a lemez, $ b $ - rétegvastagság.
Feladat: Mi legyen az ék dőlésszöge, ha a normális előfordulási monokromatikus fény hullámhossz $ \ lambda $ közötti távolság a szomszédos beavatkozás minimumok a visszavert fény egyenlő $ \ háromszög x $?
A leírt helyzet a probléma, amelynek középpontjában az 1. ábrán is írt, hogy:
ahol a $ tg \ alpha \ approx \ alpha \ $, mint az ék látószög nagyon kicsi, $ \ háromszög x $ - távolság a szomszédos minimumok. Ebben az esetben, az optikai útvonal különbséget lehet meghatározni:
Ellenkező esetben, az optikai útvonal különbséget lehet kifejezni:
\ [\ Triangle = \ left [2 \ bal (m + 1 \ right) +1 \ right] \ Frac \ bal [2M + 1 \ right] \ frac = \ lambda \ \ left (m = 0,1, 2 \ dots \ right) (1.3). \]
Mi egyenlőségjelet tesznek a jobb oldalán a kifejezést (1.2) és (1.3):
expresszáinak H egyenlet (1,4), kapjuk:
Behelyettesítve a kifejezés a h képlet (1.1), megkapjuk a kívánt szög:
Feladat: Ha a minimális vastagságú sík fóliát párhuzamos oldalai, amelynek törésmutatója megegyezik $ n> 1 $, egy párhuzamos fénysugár a fehér fény beeső a film szögben $ \ alpha = 45<>^ \ Circ, $ reflexió lesz hullámhossz egyenlő $ \ lambda $.
Írunk a feltétellel, legfeljebb az interferencia:
\ [\ Triangle = m \ lambda \ at \ m = 0,1,2 \ dots \ left (2,1 \ jobbra). \]
Annak érdekében, hogy megtalálják azt a kifejezést úthossz különbség a beavatkozás feltörekvő gerendák fordulnak ábra. 3.
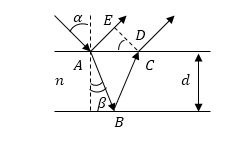
Ábra. 3, figyelembe véve a veszteség a hullámhossz fele, amikor a fény visszaverődik a optikailag sűrűbb közeg lehet írva:
Nyilvánvaló, hogy $ AB = BC $ és ábra. 3, hogy:
Az azonos szám. 3, van:
\ [AD = d \ cdot tg \ beta, \ AE = 2d \ cdot tg \ left (\ beta \ right) \ left (2,4 \ jobbra). \]
Behelyettesítve a kifejezések (2.3) és (2.4) a (2.2):
Összhangban a fénytörési törvény felírható:
Ebben az esetben a $ tg (\ beta) $ lehet meghatározni:
A $ m = 1 $ szempontjából a maximális interferencia (2.1), és az expressziós (2,5) van:
Kifejezik a kívánt kifejezés értéke (2,8), kapjuk:
Végül a minimális rétegvastagság, van: