A rendszer segítségével a matematikai inga
Célkitűzés: A tanulmány a harmonikus rezgőmozgás törvényi
zheniya példáját matematikai inga.
Eszközök és kellékek: matematikai inga, stopper, uralkodó.
Rezgőmozgás (oszcilláció) egy olyan folyamat, amelynek során a rendszer ismételten kitér annak egyensúlyi állapot, minden alkalommal visszatér oda.
Ha ez a bevallás benyújtása rendszeres időközönként, akkor a rezgés az úgynevezett időszakos.
Ingadozások az úgynevezett szabad, vagy a saját, ha bekövetkeznek a rendszerben marad magára, miután kivették az egyensúlyi helyzet.
A legegyszerűbb eset az időszakos oszcilláció harmonikus oszciiiáiómozgásban.
Úgynevezett harmonikus rezgés, ahol az oszcilláló nagysága változik, mint a szinusz (vagy koszinusz):
um x = sin () (1)
A mechanika: x irányú elmozdulás a rezgő pont annak egyensúlyi helyzete változik, mint a szinusz (vagy cosinus)).
A maximális értéke az elmozdulás az egyensúlyi helyzetből Hmm nazyvaetsyaamplitudoy harmonikus rezgés. Az érvelés (a), amely áll a megjelölést a szinusz (vagy koszinusz). Ez az úgynevezett rezgési fázisban. a - a kezdeti szakaszban (t = 0). Az érték az úgynevezett gyűrűs jelentése harmonikus rezgés:
A mennyiség T a rezgési periódus alatt - egy teljes kolebaniya-, értéke = 1 / T (Hz) - oszcillációs frekvencia - a rezgések száma egységnyi idő alatt.
Pillanatnyi sebesség harmonikus rezgés
V = = hm cos (t + O) (3)
Gyorsulás. a = - 2 um sin (t + o) = - x 2 (4)
2. egyenlet + x = 0 (5)
Ez az úgynevezett differenciális egyenlet harmonikus rezgések. A megoldás Ennek az egyenletnek a formában (1).
A harmonikus oszcilláció áll elő az erő
F = ma = - m 2 x = - kx. ahol k = m 2. (6)
arányos az elmozdulás és irányított egy egyensúlyi helyzetbe. Lehet például rugalmas erő (rugó egyensúly). Visszaállító erők is más, nem rugalmas jellegű. Ezekben az esetekben (matematikai inga) nevezzük kvázieiasztikus erők (a latin kvázi - mintha, állítólag).
Mivel k = m = 2. A harmonikus rezgés időszakra lehet kiszámítani a következő képlettel
Tekintsük a mechanikai rezgő rendszer matematikai inga.
Matematikai inga nevezzük anyagi pont, sub felfüggesztve egy súlytalan és nyújthatatlan szál - az 1. ábra.
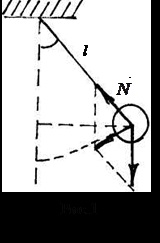
azaz a kis alakváltozás szögek erők okozó rezgések lesz arányos elmozdulását irányul, hogy a egyensúlyi helyzetben, és így az inga oszcilláció lesz harmonikus.
Tekintettel arra, hogy a = mg / l. az időszak oszcilláció a matematikai inga lehet kiszámítani a következő képlet segítségével:
(8) az következik, hogy az időszak oszcilláció a matematikai inga hosszától függ L az inga és a g nehézségi gyorsulással. de ez nem függ a tömege m az inga és a oszcillációs amplitúdóját xm
LEÍRÁS TELEPÍTÉS ÉS MÉRÉSI MÓDSZER
Miután úgy döntött, az időszak az oszcilláció a matematikai inga ismert hosszúságú lehet számítani a nagysága a gravitációs gyorsulás a Föld (a nehézségi gyorsulás függ a földrajzi szélesség) a következő képlet
Inga használunk ebben a munkában egy masszív ballon kis sugarú (szemben a hossza az inga), felfüggesztve kettős szál lehetséges ingadozások történt szigorúbban egy síkban. A távolság a felfüggesztési pont az inga a padlóra L = W, 20 m, a sugár a labdát R = 3,95 cm.
ORDER TELJESÍTMÉNYÁLLANDÓSÁG
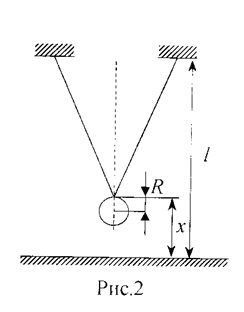
1. hosszának meghatározására az inga. Erre az intézkedésre a távolság a padlótól a tetején a labda (lásd 2. ábra). Számítsuk ki a hossza az inga képletű
Tárolja az eredményt a táblázatban