A megoldás egyszerű trigonometriai egyenlőtlenségek példák és algoritmusok
legfontosabb nbsp> nbsp Wiki-bemutató nbsp> nbsp Matematika nbsp> nbsp10 osztály nbsp> nbspReshenie egyszerű trigonometrikus egyenlőtlenségek: Példák és algoritmusok
Egyenlőtlenségek bevonásával trigonometrikus függvények, kezelése a egyenlőtlenségek csökkennek a legegyszerűbb típusú cos (t)> a, Sint (t) = A és a hasonlók. És még a legegyszerűbb egyenlőtlenség megoldását. Tekintsük a különböző példák legegyszerűbb módon megoldani trigonometrikus egyenlőtlenségeket.
1. példa Hogy oldja meg a egyenlőtlenség sin (t)> = -1/2.
Rajzolj egy egységnyi kör. Mivel sin (t) definíció szerint - egy koordináta y, vegye figyelembe, az a pont az y-tengelyen az y = -1/2. Felhívjuk rajta párhuzamos vonal az x tengely. A csomópontok Az egyenes a menetrend az egység kör jelzi azt a pontot Pt1 és Pt2. Mi csatlakoztassa a két szegmens a származási, hogy a pont Pt1 és Pt2.
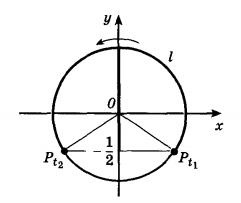
A megoldás ez az egyenlőtlenség lesz az összes pontot a készülék felett elhelyezett körbe adatokat. Más szóval, a döntés lesz az ív l. Most meg kell határozni azokat a feltételeket, amelyek mellett egy tetszőleges pont is tartozik egy ívet l.
PT1 a jobb félkör, annak ordináta egyenlő 1/2, majd t1 = arcsin (-1/2) = - pi / 6. felírhatjuk a következő képlet írja le a pontot Pt1:
t2 = pi - arcsin (-1/2) = 7 * pi / 6. Ennek eredményeként megkapjuk t a következő egyenlőtlenség:
Fenntartjuk a egyenlőtlenség jeleket. És így függvényében a szinusz függvény periodikus, akkor a döntés meg kell ismételni minden 2 * pi. Ez az állapot, majd a kapott egyenlőtlenség t és írd a választ.
Válasz: -pi / 6 + 2 * pi * n <= t <= 7*pi/6 + 2*pi*n, при любом целом n.
2. példa megoldásához az egyenlőtlenséget cos (t) <1/2.
Rajzolj egy egységnyi kör. Mivel definíció szerint, cos (t) a X-koordináta, a megjegyzés a grfike Ox pont x = 1/2.
Felhívjuk ezen a ponton keresztül egy párhuzamos egyenes az y tengelyen. A csomópontok Az egyenes a menetrend az egység kör jelzi azt a pontot Pt1 és Pt2. Mi csatlakoztassa a két szegmens a származási, hogy a pont Pt1 és Pt2.
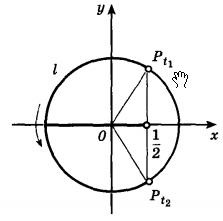
A döntések az összes pontot a készülék kör, amely tartozik egy ívet l. Megtalálni azt a pontot a T1 és T2.
t1 = arccos (1/2) = pi / 3.
T2 = 2 * pi - arccos (1/2) = 2 * pi-pi / 3 = 5 * pi / 6.
Kapott egyenlőtlenség t: pi / 3 Mivel a koszinusz - ez a funkció az időszakos, majd az oldatot meg kell ismételni minden 2 * pi. Ez az állapot, majd a kapott egyenlőtlenség t és írd a választ. Válasz: pi / 3 + 2 * pi * n 3. példa megoldásához tg (t) egyenlőtlenség <= 1. tangense idő megegyezik pi. Mi megoldást találni, hogy tartozik az intervallum (PI / 2 pi / 2), a jobb félkört. Ezután a periodicitás az érintő, írunk az összes megoldást az egyenlőtlenség. Rajzolj egy kört egység és jelölje rajta a sor érintők. Ha t lesz megoldást az egyenlőtlenség, az ordináta a T pont = tg (t) kisebbnek kell lennie, vagy egyenlő, mint 1. A pontok halmaza alkotja a sugarat. A pontok halmaza Pt, ami megfelel majd a pontok a gerenda - arc l. Sőt, a P pont (PI / 2) nem tartozik ennek az ívnek. A körülmények, amelyek a Pt bizonyos ponton fog tartozni egy ív l. t1 = arctg (1) = pi / 4. Kapjuk egyenlőtlenség -PI / 2 Tekintettel az időszak tan írási választ. Válasz: -pi / 2 + pi * n
Segítségre van szükségem az iskolában?
Kapcsolódó cikkek