A megjelenése és fejlődése a valószínűségszámítás, mint tudomány - studopediya
Még kezdetleges vezetője rájött, hogy egy tucat vadász „valószínű” sújtotta a lándzsa bölény sokkal több, mint egy. Ezért vadászott azután együttesen.
Felületesen gondolhatnánk, hogy olyan ősi polkovod-tzu, mint Nagy Sándor, vagy a Dmitry Donskoi, a felkészülés a harcra, támaszkodhat kizárólag a vitézség és ügyességi katonák.
Kétségtelen, hogy ezek a megfigyelések alapján és katonai vezetői tapasztalat tudtak valahogy értékelni a „valószínűség” az ő visszatérése „pajzs”, vagy „a fedélzeten”, tudták, mikor kell harcolni, ha elkerülni. De még mindig nagyon messze van az elmélet a valószínűség.
Később, tapasztalat, az emberek egyre inkább elkezdte tervezni az esemény nye események - megfigyelések és kísérletek, hogyan minősítik, iskho-dy lehetetlennek, lehetséges és hiteles. Észrevette, hogy a balesetek nem olyan ritkán fut objektív törvényszerűségek-ség. Itt van egy egyszerű élmény - lök egy érmét. Veszteség címer vagy számok, természetesen, pusztán véletlen jelenség. De sokszor a normális pénzfeldobás is látható, hogy a megjelenése a címer mintegy felében fordul elő az esetek. Tehát, az eredmények érme dobás, bár mindegyikük etsya véletlen esemény, ismételt ismétlése alárendeltje HN objektív törvény. Azok részére, akik rajong IP-útvonal, nagy a kísértés, hogy felhalmozódnak több jogszabályok méreteit, majd felépíteni egy elmélet őket.
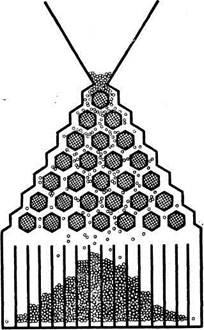
Tekintsünk egy másik, bonyolultabb például - Kísérlet úgynevezett board Galton (6. ábra). Board feltöltött hitet tikalno. A felső tározó acélgolyók tekercs (szakaszonként esik) lefelé, és felhalmozódnak az alsó foglalat.
Minden gyöngy, találkozás úton next-Px következtében eltér, vagy balra vagy jobbra, majd leesik. A labda természetesen esnek a nyílások bármelyike.
Eközben a helyes elhelyezése a golyók (szimmetrikus, amelyben a központi fészkek sok, de nagyon kevés), megismételjük az előbbi kísérletek A kísérlet Ube-clusive bizonyíték sous-létezésének objektív-Kona forgalmazás. Amikor a labda egy csomó, azt mondják, hogy forgalmazza a rendes törvény-Term.
Így esélye lehet al-javítás viszonylag egyszerű és bonyolultabb törvényszerűségek-Cham. De a kérdés az, hol van a matematika, ahol matematikai problémák?
A legérdekesebb az on-Chin problémák valószínűségszámítás alakult ki a területén szerencsejáték-CIÓ játékokat, de a formáció elveinek valószínűségszámítás spo-sobstvovali tisztázzák az élettartam, a népesség száma, gyakorlat, biztosítás-CIÓ. A szerencsejáték tulajdonítható dobott hex igral-CIÓ csont. [1] On-például dobált két fonat-tei nehéz ( „veszély”) a megjelenése összesen két-két pontot, a Tizenkét.
Miután közel ötven éve, egy másik olasz matematikus D. Cardano (1501-1576) vetjük érvek Pacioli tisztességes üvöltését kritika, de azt javasolta, hogy a hibás döntést.
Beletelt egy 100-plus éve, és 1654-ben az volt a probléma a végén megoldott során levelezés két kiváló matematikus tsuzskimi Fran B. Pascal (1623-1662) és a Fermat (1601-1665).
Ez az első alkalom az alapjait valószínűségszámítás rakták a nyomon következően a francia matematikus, Pierre Simon de Laplace (1749-1827) című könyvében: „Analitikai elmélet a valószínűség.”
Laplace nem láthatta előre, hogy el fog tartani egy pár tíz lety és érdeklődés az elmélet a valószínűség csökken. És valójában mi történt. Az év második felében a XIX század és XX század elején neko-torye matematika nem érdekli valószínűségszámítás, mint egy matematikai fegyelem.
Mi magyarázza ezt a közönyt néhány matematikusok a valószínűség elmélete? Ennek számos oka lehet. De itt nyitunk egyetlen.
A valószínűsége az esemény határoztuk meg Laplace az alábbiak szerint:
ahol n - az összes egyformán események, a m - azok száma, esemény fordul elő, amikor a kívánt eredmény ( „előnyben esemény”).
Úgy tűnik, hogy minden rendben van - a Laplace definíciója valószínűségi események nem találtunk hibát. De a kérdés az, hogy mikor és milyen véletlen események mindegyike egyaránt lehetséges?
Egy gyermek születik. Fiú vagy lány - úgy tűnik, egyformán valószínű események (az egyik, mint a dobás egy érme). De kiderül, hogy a születés statisztikák nem teljesen összhangban van a „think”.
Ez lehet, például, a következők szerint:
Ha különböző időpontokban különböző országokban, több fiú születik, mint a lányok, így a valószínűsége, hogy a születés egy fiú vagy lány egyenlőtlen: a valószínűsége az esemény „kisfiú” többé.
Emlékezzünk a pénzfeldobás (lásd. Fölötte). Hol van abban, hogy a valószínűsége fejüket, amikor essek végtelenül ismétlődő, egyenlő?
Tényeket, amelyek azt mutatják, hogy az objektív valóság nem feltétlenül esik egybe az emberi „úgy tűnik”, okozta kétségek a legitimitását a „ugyanúgy lehetséges eseményeket.” Szükség volt az „újra megvizsgálja” a valószínűsége annak, hogy kiszámított Laplace egyenlet. kísérletek.
Rendíthetetlenül védte a pozícióját az elmélet a valószínűség magyar társ-Matic. 1846-ban a szentpétervári Tudományos Akadémia kiadott egy könyvet V. Ya. Bunyakovskogo (1804-1889), melynek címe „alapjai társ-matic elmélet a valószínűség.” Ez volt az első magyar tankönyv valószínűségszámítás. Rajta ment, és a kiemelkedő magyar ma témák P. L. Chebyshev. Bár ő írta az elmélet a valószínűség nem annyira működik, de azok továbbra is kiemelkedő zna-chenie napjainkig. Az úgynevezett P. L. Chebysheva egyenlőtlenség sem lépett be a kincstár a matematikai tudományok.
Diák P. L. Chebysheva A. A. Markov kifejlesztett fejti ki uchi tell. Neki tartozik a dicsőség a felfedezője a fontos alkalmazások valószínűségszámítás - az elmélet a valószínűség, vagy sztochasztikus folyamatok.
A öröksége a magyar matematikus fejlesztette a munkálatok szovjet matematikusok EE Slutsky, SN Bernstein, AJ Khinchin, Y. Linnik különösen akadémikus AN Kolmogorov. létre Kolmogorov szovjet iskola valószínűségszámítás szerzett elismerést és ma egy vezető pozícióját a világ tudományos.