A mátrix egy lineáris operátor

előző ◈ a következő

Legyen egy lineáris operátor

, transzformáló xL1 in yL2:

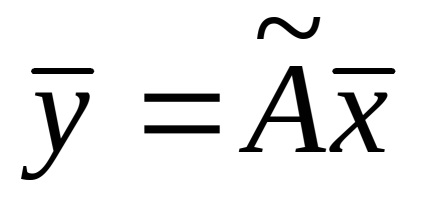
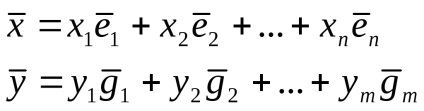
Ie beállítani az üzemeltető elegendő megadni csak a képek alapján vektorok, azaz

e1,

e2. ...,

HU.

Tegyük fel, hogy ezek a képek

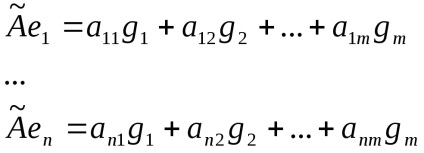
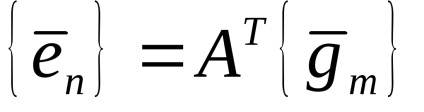
Ezután következik a fenti:

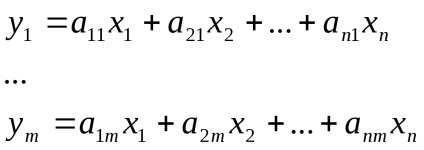
A mátrix átültetés A T egy mátrix egy lineáris operátor, K-edik oszlopa a mátrix összetétele a vektor koordinátákat

EK alapján G1 G2 ... gm.

Kiderült, hogy néhány jellemzője ennek a mátrix nem függ a bázisok és jellemzik a belső tulajdonságait az üzemeltető. Így írunk bizonyíték nélkül, hogy a rang a mátrix egy lineáris operátor megegyezik a dimenzió a tér a képek. Fogjuk hívni ezt a rangot - rangot lineáris operátor. Ha ez a rang megegyezik a mérete a tér L vagy dimenziója a tér egybeesik a dimenzió az inverz képek a tér, az üzemeltető

az úgynevezett nem-degenerált.

Ha a beállított képek és sor inverz képek tartoznak azonos térben, fogunk beszélni az átalakulás a tér önmagába és az üzemeltető a konverziós operátor fogják hívni lineáris transzformáció vagy lineáris operátor. A jövőben, figyelembe vesszük a lineáris szolgáltatók és a kifejezés használatára.

Megváltoztatása lineáris operátor mátrix

az átállás során egy alapon a másikra.

Már említettük, hogy a mátrix a lineáris operátor függ alapján. Azt a kérdést, hogyan függ a mátrixot alapján általában. Hagyja, hogy a kezelő készlet y =

Egyes alapján ez megfelel egy lineáris transzformáció Y = AX.

Bemutatjuk az új alapot. Ha az átmeneti mátrix T, akkor X = TX * Y = TY *.

Így van egy TY * = ATX *; Y * = T -1 ATX *.

Vagy Y * = A * X *; A * = T -1 AT.

Megjegyezzük, hogy az A mátrix és A * azt mondják, hogy hasonló (T - nonsingular mátrix).

Sajátvektor és sajátérték

Nemnulla x vektor nevezzük sajátvektorának lineáris operátor

, ha van chislo hogy az egyenlőség:

X = h.

Száma nazyvaetsya saját számát, illetve sajátérték

mert operátor

Ez átalakítja a teret is, a mátrix az üzemeltető téren. Ha egy alapja n>, a

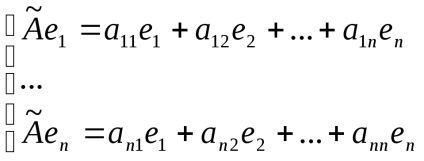
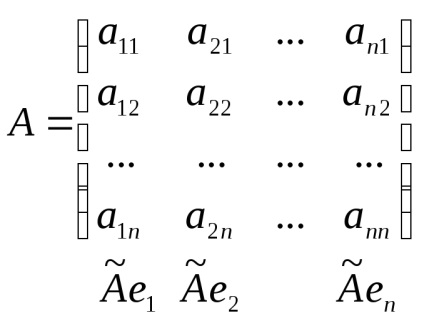
Írt a koordináta formájában egyenlőség

X = h:

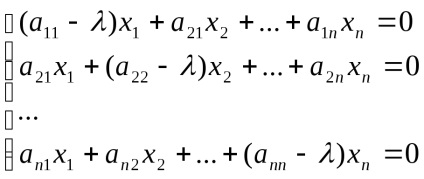
Ez a rendszer a lineáris homogén egyenletek az x koordinátája a kívánt vektor. mert X 0, a rendszer egy nem-zéró oldatot. Ennélfogva, e célból, legyen det (A -E) = 0, vagy a

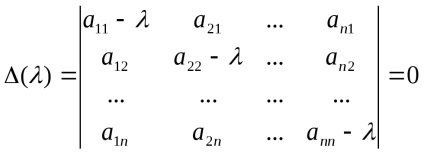
Az egyenlet  () = 0 nevezzük a karakterisztikus egyenlet lineáris operátor

, és a polinom

N fok relatív - karakterisztikus polinom.

Az algebra alaptétele, minden polinom foka n n gyökerei sokszorozódással. Ennélfogva, a karakterisztikus egyenlet legalább egy gyökér, azaz Minden üzemeltetőnek legalább egy sajátvektor. Igaz, a valós térben polinom nem lehet valódi gyökereit, és ezért a mi lineáris térben minden lineáris operátor sajátvektor.

így hogy meghatározza a sajátvektor van, hogy a karakterisztikus polinom, megtalálja a gyökereit, amelyek a sajátértékek. Akkor kell minden sajátérték i helyettesítő vmestov rendszer, és megtalálja az összes lineáris - független megoldásokat. A számos ilyen oldatra, n - ri. ahol ri - rangot A mátrix -i E. Ebből következik, hogy a dimenziója a sajátvektorok megfelelő saját chislui egyenlő n-nel - ri.

Emlékezzünk, hogy a mátrix a lineáris operátor változik a bázis:

hogy van-e alapja, amelyben a mátrix * volna egy átlós? A következő tétel érvényes: a matritsaA az adott alapot ek> diagonális, szükséges és elégséges, hogy az alapvető vektoryek volt sajátvektorait ennek az operátornak.

Bizonyítás: Legyen ek sajátvektorai operatoraA. majd

Ezért az A mátrix formában van must

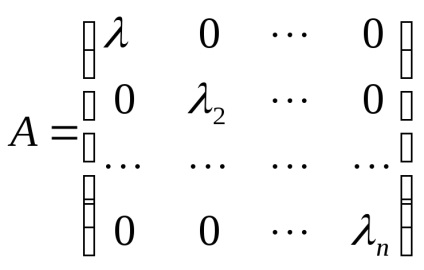
és fordítva. Legyen - diagonális mátrix az üzemeltető az alapon ek>. Aztán sootnoshnniya

formájában (*), ami azt jelenti, hogy ek - sajátvektor.

Írunk és nincs bizonyíték a lineáris operátor tulajdonság, hogy a sajátvektorait lineáris operátor megfelelő különböző sajátértékek lineárisan függetlenek.

Definíció. hívás operátor. mátrixot csökken átlós formában, az egyszerű szerkezet a kezelő. Írunk bizonyíték nélkül, hogy az üzemeltető egy egyszerű szerkezet két esetben: 1) a karakterisztikus polinom imeetn különböző gyökerek; 2) az egyes kornyai kratnostiki rangot a mátrix (a -iE) volt ravenn-ki.

Nézzük meg, mi az a meghatározó a mátrix lineáris üzemeltető a változás alapján.

det (A *) = det (T -1 AT) = det (T-1) det (A) det (T) = det (A) det (T -1 T) = det (A) det (E) = det (A)

Így elmondható, hogy az érték a meghatározó a lineáris operátor nem függ a választott alapon. Ahhoz, hogy megtalálja a sajátértékek a lineáris operátor voltunk karakterisztikus polinom

Mivel az érték a meghatározó nem függ a választott alapon a velichinydk vannak invariánsokra - nem függ alapján. Ez az úgynevezett együttható pri n -1: dn-1 = A11 + A22 + ... + Ann nyomkövetési operatoraA és oboznachattrA (trace- nyomnyi).

Ez könnyű nyomon követni a kapcsolatát invariánsokra konvertáló koordináta rendszerek, állunk szemben a transzformációs egyenletek másodrendű felületek:

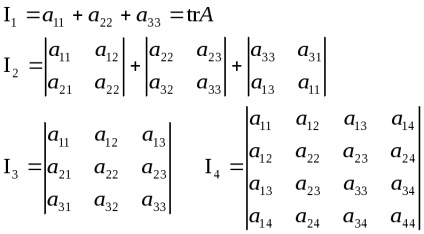
dk együtthatók és a karakterisztikus egyenlet lineáris szereplő háromdimenziós térben. N = 3 Ezt szem előtt tartva, írhatunk kényelmes formulát találni a karakterisztikus egyenlet lineáris üzemeltető lép a háromdimenziós térben:

Kapcsolódó cikkek

előző ◈ a következő