A magasabb matematika, torony
5.1. alapfogalmak
Az értékek teljesen határozza meg a számértéket, úgynevezett skalár. Példák a skalár mennyiségek: terület, hosszúság, térfogat, hőmérséklet, a munka tömege.
Más értékek, mint erő, sebesség, gyorsulás, az határozza meg nem csak a számszerű érték, hanem az irányt. Ezeket az értékeket nevezzük vektor. Geometriailag képviseli vektor mennyiség egy vektor.
Vektor - egy irányított vonal szegmenst, azaz, a szegmens, amelynek egy bizonyos hosszúságú, és egy bizonyos irányba ... Ha A - az elején a vektor, és a B - a vége, akkor a vektort nevezzük AB vagy szimbólum. Vektor BA (ő kezdődő B pontban és véget ér A pont) nevezzük ellentétes vektor AB. Vektor, és a szemközti vektor. Ez azt jelenti - a.
Hossz vagy egy modult a vektor AB nevezzük a hossza a szegmens és jelöljük | AB |. A vektor hossza egyenlő nullával az úgynevezett nulla vektor, és jelöljük 0. A nulla vektor irányát nem számít.
Vektor, amelynek hossza megegyezik az egyik az úgynevezett egy egységvektor, és jelöljük e. Az egység vektor, amelynek iránya egybeesik az irányt a vektor egy. Ez az úgynevezett egység vektort a vektor és a jelöli a °.
A és b vektorok nevezzük kollineáris ha fekszenek ugyanabban a sorban vagy párhuzamos vonalak; rögzítése || b.
Kollineáris vektorok lehetnek azonos vagy ellentétes irányú.
Nulla vektor minősül minden vektor esik.
Két vektort a és b nevezzük egyenlő (a = b), ha azok egy egyenesbe esik, ugyanabban az irányban, és az azonos hosszúságú.
A meghatározása az egyenlő vektorok, hogy a vektor lehet mozgatni önmagával párhuzamosan, és az elején a Vector elhelyezett bármely pontján a teret.
Az 1. ábrán, a vektorok egy téglalap. A egyenlőség b = d. de egy ¹. A vektorok a és - ellentétben, a = - p.
Egyenlő vektorok nevezzük szabad.
Három vektortérnek nevezzük egy síkban vannak. ha hazudnak ugyanabban a síkban vagy párhuzamos síkokban. Ha a három vektorok legalább egy nulla vagy kettő minden kollineáris, az ilyen vektorok egy síkban
5.2. Lineáris műveleteket vektorok
Kevesebb lineáris műveleteket vektorok megérteni a működését az összeadás és kivonás, vektorok, majd megszorozzuk a vektor egy szám.
Legyenek a és b - két tetszőleges vektorok. Vegyünk egy tetszőleges pont O és vektort OA = a. Pont a defer vektor AB = b. Vector OB. összekötő elején az első vektor a második vége, az úgynevezett összege a és b vektorok. O B = a + b (lásd. Ábra. 2)
.
Ez a szabály az úgynevezett jogállamiság vektor felül háromszög. Összege két vektor is kialakítható a szabály alapján a párhuzamos o gramm (lásd. Ábra. 3.).
A 4. ábra a további három vektorok is. b, és c.
Az a különbség vektorok és az átlagos vektor b és c = a - b úgy, hogy b + c = a (lásd 5. ábra ..).
Megjegyezzük, hogy a paralelogramma-épített a a és b vektorok, az egyik átlói mentén az összege az a és b vektorok, és a másik - a különbség (lásd 6. ábra ..).
Lehetőség van kivonni szerinti vektorok a szabály: a - b = a + (- b), azaz, a mellett kivonás vektorok a vektor és a helyére egy vektorral szemben, hogy a b vektor ...
A terméket a vektort és egy skalár (integer) # 955; Ez egy vektor # 955; * A (vagy A * # 955;), amelynek a hossza | # 955; | * | és |, az azzal egy vonalba. és azt egy irányvektor. ha # 955> 0, és az ellenkező irányba, ha # 955;<0. Из определения произведения вектора на число следуют свойства этого произведения:
1) ha a b = # 955; * A. majd a b || a. Ezzel szemben, ha b || a. (A ¹ 0), akkor valamely # 955; Az egyenlőség b = # 955; és;
2) mindig a = | és | • -o. t. e., az egyes vektor egyenlő a termék a maga modulusa az egységvektor.
Lineáris műveleteket vektorok a következő tulajdonságokkal rendelkezik:
1. a + b = b + a
2. (a + b) + c = a + (b + c),
3. # 955; 1 • (# 955; 2 • a) = # 955; # 955 1 • 2 • és,
4. (# 955, # 955 + 1; 2) • a = # 955; a + 1 • # 955; 2 • és,
5. # 955; • (a + b) = # 955; • a + # 955; • b.
Ezek a tulajdonságok lehetővé teszik átalakítására lineáris vektor műveletek ahogy az rendes algebra: a kifejezések felcserélhetők, ugorjon a zárójelek a csoportot, hogy a konzolok mind skalár és vektor közös tényezők.
5.3. A vetítés a vektor a tengelyen
A tér meghatározott tengely L, T. E. Directed vonal.
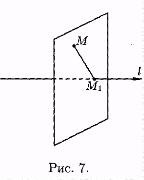
A vetítés M pont a tengelyen L nevezett bázis M1 merőleges MM1. esett egy pontot a tengelyen.
M1 pont a metszéspont a tengely l síkjával ponton áthaladó tengelyére merőlegesen M (lásd. Ábra. 7).
Ha M fekszik a tengelyen l. a vetülete az M pont a tengelye egybeesik M1.
Legyen AB - tetszőleges vektor (AB ¹ 0). Jelöljük A1 és 1 b a vetülete a tengelyen L rendre kezdeni az A és B vége vektorok AB, és megvizsgálja a vektor az A 1 B 1
Projection A vektor AB a tengelyen l azt mondják, hogy egy pozitív szám | A 1 B 1 |. ha a vektor egy 1 l 1, és hasonlóképpen utasította tengelye és a több negatív - | A 1 B 1 |. Ha a vektor az A 1 B 1 és L tengely ellentétes irányban (lásd. ábra. 8). Ha az A 1 és B 1 jelentése azonos az (A 1 B 1 = 0), akkor a nyúlvány a vektor AB 0.
A vetítés a vektor AB l tengelye jelöli pr l AB. Ha az AB = 0, vagy AB ^ l. A PRL AB = 0.
A szög j közötti a vektor egy, és a tengely L (vagy a szög két vektor) van a 9. ábrán látható Nyilvánvaló, 0 £ j £ p
Nézzük meg néhány alapvető tulajdonságait előrejelzések.
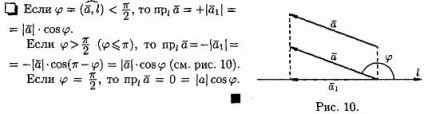
Tulajdonság 1. A vetülete egy vektor-ra a tengely L egyenlő a termék egy egységet vektor a koszinusz a szög j közötti a vektor és a tengely, azaz egy egyenes L = .. | a | • cos j.
Következmény 5.1. A vetítés a vektor a tengelyen a pozitív (negatív), ha a vektor hegyesszöget (tompaszögű) szöge a tengely, és a nulla, ha a szög - line.
Következmény 5.2. Projection vektorok egyenlő egy és ugyanazon tengely egyenlő.
Az ingatlan 2 A vetítés összege több olyan vektor azonos tengelyre egyenlő összegével előrejelzések ezen a tengelyen
Tulajdonság 3. Amikor megszorozzuk a vektor és a szám egy annak vetülete a tengelyen is számának szorzatával m. E.

Így a lineáris műveleteket vektorok eredményez megfelelő műveleteket lineáris előrejelzések e vektorok.
5.4. A bomlás a vektor az egység vektorok a koordinátatengelyek.
vektor modul. Iránykoszinuszokat.
A tér Oxyz derékszögű koordináta-rendszert. Kiválasztjuk a koordinátatengelyeken Ox, Oy és Oz egység vektorok (alap vektorok) bekezdésében említett, i. j. k, illetve (lásd. ábra. 12).
Válasszon egy tetszőleges vektor egy teret, és ez összhangban van felső eredetű: a = OM.
Megtaláljuk a vetülete a vektor és a koordináta tengelyekkel. Keresztül a végén a vektor OM sík párhuzamos a koordináta síkon. A metszéspontjai ezek a síkok a tengelyek jelöljük az M 1 és M2 Mz.Poluchim derékszögű parallelepipedon, az egyik átlós amelyek vektor OM. Stb Aztán x = a | OM 1 | NPY a = | OM 2 |, stb és z = | OM s |. A meghatározás szerint az összege több vektorok találni = 1 OM + M1 N + NM.
Mivel M 1 N = OM 2. NM = OM s, majd
Jelöljük a nyúlvány a vektor a = OM Ox, Oy és Oz rendre keresztül ah. ay és az AZ. azaz | OM 1 | = Ax, | OM 2 | = Ay. | OM 3 | = A Z. Ezután következik (5,1) és (5,2)
Ez a képlet a fő vektor, és a számítási nevezzük bomlása vektort az egység vektorok a koordinátatengelyek. A több ah. ay. AZ koordinátákat nevezzük vektor egy, t. e. a koordinátáit a vetítés áll a megfelelő koordináta tengelyt.
A vektor (5.3) egyenlete gyakran írva egy szimbolikus formában: a = (ax; Ay; Az).
B = (bx; által; bz) azt jelenti, hogy b = b x • i + b y • j + bz • k. Ismerve a komponensek a vektor egy. könnyen megtalálja a kifejezést a vektor egység. Alapján a tételt az átló hosszát egy téglatest írhat
t. e. egyenlő a nagysága a négyzetgyöke a négyzetének összege annak nyúlványok a tengelyekre.
Legyen egy vektort szögek a tengelyek Ox, Oy és Oz rendre a, b, g. Az ingatlan a vetülete a tengelyen, van
Vagy ami ugyanaz,
A számok az úgynevezett iránykoszinuszokat a vektor egy.
Mi helyettesíti kifejezést (5.5) a (5.4), megkapjuk
Csökkentése, így a kapcsolat
t. e. a négyzetének összege a iránykoszinuszokat nemnulla vektor egyenlő eggyel.
Ez könnyű észrevenni, hogy a koordinátákat a készülék vektor e számok
Így azáltal koordinátáit a vektor mindig lehetséges, hogy meghatározza annak nagyságát és irányát, azaz, vektor maga.