A legegyszerűbb alkalmazás flow
Az események menetébe úgynevezett egyszerű (vagy stacionárius Poisson), ha csak három tulajdonságok: helyhez kötött, és nem rendes utóhatások. A név „legegyszerűbb” annak a ténynek köszönhető, hogy a kapcsolódó folyamatok elemi stream, leginkább egyszerű matematikai leírása. A legegyszerűbb, első pillantásra, a rendszeres áramlását nem „bocsáss meg”, mivel van egy utóhatás: pillanatában előfordulása, mint esemény flow kapcsolódó merev funkcionális függőséget. Anélkül különleges erőfeszítéseket, hogy megőrizze szabályszerűségét olyan áramlási általában nem jön létre.
A legegyszerűbb áramlási különleges szerepet játszik a többi között a szálakat. Nevezetesen, kérelemre (szuperpozíciója) egy kellően nagy számú független, helyhez kötött és a közönséges folyamok (összehasonlíthatók egymással intenzitás) kapunk áramlási közel a legegyszerűbb.
Egy egyszerű áramban intenzitású intervallum l közötti szomszédos események az úgynevezett exponenciális (exponenciális) eloszlású sűrűségű
ahol l - paraméter exponenciális törvény
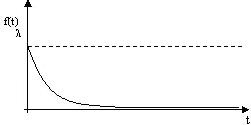
Ábra. 1.9.2 ütemterve sűrűség eloszlását az exponenciális eloszlás
Egy véletlen változó T rendelkező exponenciális eloszlás, a várakozás mT a reciproka a paraméter, és a standard eltérés egyeznie az átlagos sT:
A valószínűségszámítás, mint egy „intézkedés véletlenszerűség” nem-negatív véletlen értéket gyakran tekintik úgy nevezett variációs együttható:
A képletek (2), (3) az következik, hogy az exponenciális eloszlás nt = 1, t. E. Az áramlási események legegyszerűbb variációs koefficiense intervallumok közötti események az egység.
Nyilvánvaló, hogy a rendszeres áramlásának események, amelyek a közötti időszakban az események nem véletlen egyáltalán (nt = 0), a variációs koefficiens értéke nulla. A legtöbb áramlási események a gyakorlatban előforduló, a variációs együtthatója között eltelt események zárt nulla és egy között, és szolgálhat olyan intézkedés, a „fok szabályosság” flow: nt közelebb a nullához, a „rendes” áramlását. Egyszerű patak - a „kevésbé szabályos” -tól a gyakorlatban előforduló folyik.
A számítások kapcsolódó események menetébe, nagyon kényelmes a használata a „eleme a valószínűség.” Tekintsük az időtengelyen egy egyszerű áramlási intenzitást l és önkényesen elhelyezve elemi (nagyon kicsi) része idő Dt.
Elemei valószínűsége a valószínűsége, hogy ezen időtartam legalább egy patak az események. Ez könnyű bizonyítani, hogy a valószínűsége az elem (eltekintve kis mennyiségű magasabb rendű Dt) egyenlő:
t. e. egy egyszerű adatfolyam elemet valószínűsége egyenlő az áramlási sebesség szorozva az elemi intervallum hossza. Elemei valószínűsége, mivel a hiányzó utóhatás, nem attól függ, hogy hány esemény, és ha nem volt korábban.