A koordinátáit a tömegközéppont
§ 2.12. A koordinátáit a tömegközéppont
A hely, ahol a bevezetett derékszögű koordináta-rendszert, legyen az anyagi pont van beállítva tömeg. Statikus pillanatában ezen a ponton síkhoz viszonyítva a termék a, és jelöljük
A statikus pillanat viszonylagos anyagi rámutat véges rendszer által meghatározott sík tömegek
Végül, ha a tömeg eloszlik egy bizonyos, a statikus pillanat a test síkjához képest meghatározott integrál,
ahol - sűrűsége tömegeloszlású.
A test súlypontjának koordinátái által meghatározott egyenletek
Különösen, ha van egy görbe vonalú trapéz síkban korlátos felett és alatt a függvény grafikonját tengely, egyenletesen megtöltött tömegsűrűsége, a (Fig.57)
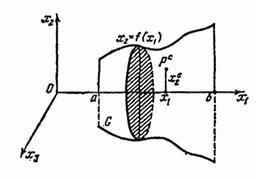
A jobb oldali rész (1) a térfogata a test kapott a forgástengelytől körül ívelt trapéz.
Így van a jól ismert tétel Gyuldina: forgástest térfogata görbe vonalú trapéz megegyezik annak területe szorozva a hossza a kör által leírt tömegközéppontja (gravitációs) a trapéz tengely körül.
Ha van egy egységes görbe,
ahol - a hossza a görbe tartományban - ívhossz elem. Azóta
A jobb oldali rész (2) az a terület, a forgásfelületen tengelye körül a görbe. Így, (2) egyenlet ad egy másik tétel Gyuldina: felülete a görbe forgási hosszával megegyező annak ív, szorozva a hossza a kör által leírt a tömegközéppontja az ív tengely körül.
Tételek Gyuldina hogy két ismert értékeket találni a harmadik. Például, ha az ismert koordinátáit a súlypont és az összeget a test forgásának, lehetőség van, hogy meghatározzuk a területet a görbe trapéz, és így tovább. D.
1. példa megtaláljuk a koordinátákat a súlypontja az ívelt trapéz (ábra. 58).
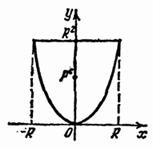
Hagyja, - a súlypont. Szimmetria, egyértelmű, hogy (azt hiszem). Keresse meg a terület trapéz:
A kötet a test nyert forgási tengely körül van
Ennek alapján az első tétel Gyuldina
2. példa Find a térfogata a kapott szilárd anyagot forgó kör közepén a ponton sugara, tengely körül (ábra. 59).
Egyértelmű, hogy a súlypont a kör (homogén) egybeesik a geometriai középpont, azaz a. F .. terület a kör. Ezért az első tétel Gyuldina
3. példa Find területén forgását a testfelület, a 2. példában leírt.
Ez a felület lehet tekinteni, mint egy felszíni által generált forgó kör tengelye körül. A hossza a kerülete egyenlő. Ezért a második tétel Gyuldina
(Egységes kerületi súlypontja egybeesik az a kör közepén).
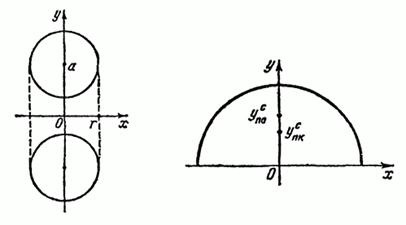
4. példa Find a súlypont homogén félkör; félkört.
Ismeretes, hogy a kötet egy gömb sugara egyenlő lehet, és egyenlő a felülete a labdát. A képlet szerint (1) kapjuk (ábra. 60)
ahol - ordináta a súlypont a félkör.
A képlet szerint (2) a súlypontja az ordináta van félkör
Pillanatokat. Th momentum egy anyagi pont masszát síkjához képest a termék a
Ha a tömegek vannak elosztva mérhető halmaz a sűrűség,
Ha a megfelelő pontot nevezzük másodrendű tehetetlenségi nyomaték.
Sőt, mondhatjuk test -ik érdekében pillanatok eredete
tengelyéhez viszonyítva. Például a pillanat ahhoz képest a tengelyre felírható