A koncepció a partíció az osztályok 1
A fogalmak készletek és állítsa műveletek lehetővé teszik számunkra, hogy finomítani, hogy megértsük a besorolás - a jelenlegi elosztása tárgyak osztályok.
Besorolás mi elég gyakran. Például a természetes számok a két osztály - a páros és páratlan. A szögeket a síkban három kategóriába sorolhatók: a közvetlen, éles és tompa.
Bármilyen besorolás összefügg a osztályfelbontás tárgyak alszettekre. Feltételezzük, hogy X osztályokra oszlik X1. X2. Xn. ha:
2) kombinálásával részhalmazok X1. X2. X egybeesik a beállított X.
Ha nem elégedett, legalább az egyik feltétel, az osztályozás minősül. Például, ha az X halmaz részhalmaza egyenlő szárú háromszögek kiemelni, egyenlő oldalú háromszög és sokoldalú, a partíciókat nem kapunk, mint egy részhalmaza egyenlő szárú és egyenlő oldalú háromszög metszik egymást (minden egyenlő oldalú háromszög egyenlő szárú). Ebben az esetben az első feltétel nem teljesül a partíció az osztályok.
Mivel a partíció osztályok kapcsolódó megjelenése részhalmaza, a besorolás is elvégezhető MRI alkalmazásával tulajdonságait halmaz elemei.
Vegyük például a természetes számok halmaza. Elemei különböző tulajdonságokkal rendelkeznek. Tegyük fel, hogy mi érdekli a számot a tulajdonság „hogy többszöröse 3”. Ez a funkció lehetővé teszi, hogy válasszon a természetes számok halmaza részhalmaza, amely a számok többszörösei 3. Ezután
a többi természetes számok azt mondhatjuk, hogy ezek nem többszöröse 3, azaz Kapunk még egy részhalmaza a természetes számok (12.). Mivel a kiválasztott részhalmazok diszjunktak és szakszervezet a természetes számok halmaza, akkor van egy partíció ez a készlet két osztály.

Általában, ha az X halmaz adott egy ingatlan, akkor ez a készlet két csoportra oszthatók. Az első osztály a tárgyak az ingatlan, és a második kívül az első osztályú, hogy a beállított X. A második osztályba sokaságát tartalmazza az ilyen tárgyak X, amelyek nem rendelkeznek az adott tulajdonság. Ez a besorolás az úgynevezett dichotóm.
Nézzük a helyzet, amikor több elemet a két tulajdonság be van állítva. Például néhány tulajdonságait a természetes számok, mint „egy többszöröse 3” és „többszöröse lesz 5.” Segítségével ezek a tulajdonságok a több N egész számok lehet megkülönböztetni részhalmaza alsó: A - egy részhalmaza többszörösei 3, és B - részhalmaza többszörösei 5. Ezek a készlet diszjunkt, de egyikük sem egy részhalmaza egy másik (13. ábra).
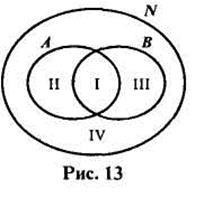
Elemezzük a kapott kép. Természetesen a partíció a természetes számok halmaza két részhalmaza az A és B nem történt meg. De a kör, mutatja a sok N, lehet tekinteni, mint amely a négy nem átfedő területek - ezek meg vannak számlálva az ábrán. Mindegyik régió képviseli egy részhalmaza N. részhalmaza I áll többszörösei 3 és 5; részhalmaza II - a többszörösei 3 vagy 5-ször; III részhalmaza -A többszörösei 5 és nem többszörösei 3; IV- részhalmaza számok nem többszörösei 3 vagy többszöröse 5. A kombináció a négy részhalmazainak halmaza N.
Így, a kiválasztás a két tulajdonság vezetett a partíció a természetes számok halmaza N négy osztályba csoportosítják.
Ne gondoljuk, hogy a munkát a két ingatlan a készlet elemei mindig vezet a partíció ez a készlet négy osztályba sorolják. Például, az ilyen két tulajdonság „többszöröse lesz 3” és „a többszöröse 6” természetes számok halmaza van osztva három osztályba (ábra. 14):
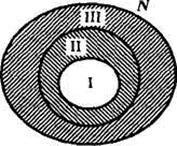
I - osztályú többszörösei 6; II - osztály többszörösei 3, de nem több 6; III - osztály szám, nem többszöröse 3.
Két számjeggyel, például 3 és 5, akkor rögzíteni négyjegyű számot: 35, 53, 33 és 55. Bár a számok 35 és 53 rögzített ugyanazokkal a számokkal, ezek a számok különbözőek. Abban az esetben, ha a sorrendben a legfontosabb eleme a matematikai beszélhetünk rendezett halmaza elemekkel. Ebben a példában foglalkoztunk a rendezett párok.
Rendezett pár kialakítva elemek a és b, általában írva zárójelek segítségével: (a; b). Egy elem egy első koordináta (komponens) a pár. és a B-elem - második koordináta (komponens) a pár.
Pár (a, b) és (c, d) egyenlő, és csak abban az esetben, ha a = c, és b = d.
A rendezett párt (a; b) olyan lehet, hogy a = b. Így, belépési szám 33 és 55 tekinthető rendezett párokat (3, 3) és (5, 5).
A rendezett párokat kialakítható elemek sokaságát egy vagy két. Tegyük fel például, = 4, B =. Képező rendezett pár, hogy az első komponens tartozik a halmaz, és állítsa B. vtoraya- Ha felsoroljuk az összes párt, akkor kap egy sor:
Látjuk, hogy van két A és B, kaptunk egy új, amelynek elemeit rendezett számpárok. Ez a készlet az úgynevezett Descartes termék az A és B
Definíció. Descartes termék az A és B jelentése a készlet minden pár az első komponens, amely tartozik, hogy hozzanak egy, és a második komponens tartozik a beállított W.
Descartes-szorzat készletek A és B jelentése Ah V. használva ezt a jelölést, a meghatározása Descartes-szorzat írható fel:
PROBLÉMA órán 1. Keresse meg a Descartes-szorzat az A és B halmaz, ha:
Határozat. a) szerint működik opredeleniyu- összes pár alkotják az első komponense közül kiválasztott egy, és a másik - B:
b) egy Descartes-szorzat halmazok egyenlő alkotnak minden lehetséges pár halmaz elemeit:
A művelet a megállapítás a Descartes-szorzat készletek hívják Descartes szorzás. Engedje meg, hogy milyen tulajdonságokkal ezt a műveletet. Mivel Descartes-szorzat A x B x és B áll a különböző elemek, a derékszögű szaporodását és B nem kommutatív. Mi lehet bizonyítani, hogy nem hajtja végre a derékszögű szorzás és tulajdonát asszociatív. De a Descartes termék elosztó tekintetében a szakszervezet és kivonás készletek, azaz bármely készletek A, B és C jelentése a egyenletet:
(A) x G = (A x C) (B x C)
(A \ B) x G = (A x B) \ (B x C).
PROBLÉMA h és 2. Ellenőrizze érvényességét elosztó tulajdonát szorzás képest derékszögű egyesület, ha:
Határozat. Találunk az unió az A és B: A = B. További elemek listája (A) X C-on, a meghatározása a Descartes termék: (A) X C =.
Ahhoz, hogy megtalálja a halmaz elemeit (A x C) (B x C), első listát a halmaz elemei a C és A x B x C:
Látjuk, hogy a beállított (A B) x C, és (A x C) (B x C) állnak, az azonos elemeket, ezért, hogy a készletek egy adat, B és C, mi (A) x G = ( A x C) (B x C).
Nézzük, hogyan lehetséges, hogy szemléltesse a Descartes-szorzat készletek.
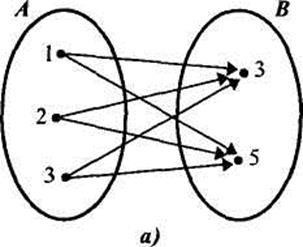
Ha a A és B halmaz végesek, és tartalmaznak egy kis számú elemet, akkor képviseli a Descartes-szorzat halmazok a diagramon vagy asztalra. Például, Descartes-szorzat készletek A = B és = úgy reprezentálható, mint a 17. ábra mutatja (a, b).
A Descartes-szorzat a két numerikus (véges és végtelen) is képviselteti magát egy koordináta síkban minden páros szám lehet egyedileg jelenik pont ezen a síkon. Például, Descartes-szorzat készletek A xB = A és B = (3, 5> a koordináta-síkban fog kinézni, hogy a 18. ábrán látható.
0 1 2 3 X 18. ábra
Megjegyezzük, hogy elemei a már látható az x tengelyen, és az elemek a készlet B - az y-tengelyen.
Így láthatóvá tesszük a Descartes-szorzat a két számsorral hasznos abban az esetben, ha legalább egyikük végtelen.
Probléma 3. mutat a koordináta síkon Descartes-szorzat Ax B, ha:
R e w n e, a) Mivel A három elemből áll, és a B halmaz tartalmazza az összes valós számok 3-5, beleértve a számok önmagukban, akkor a Descartes-szorzat A x B áll végtelen sok takarmánytárolókat az első komponens, amely 1 vagy 2 vagy 3, és a második bármilyen valós szám az intervallum [3, 5]. Az ilyen több pár valós számok a koordinátasík képviseli a három szegmens (ábra. 19).
0 1 2 3 x Fig. 19
b) Ebben az esetben a végtelenített mind az A és B Ezért, az első koordináta pár tartozó beállított Ax B bármilyen szám lehet, az [1,3], és így, a pontokat képviselő Descartes-szorzat elemeinek adatkészletek A és B, alkotnak egy négyzet (ábra. 20).
z) Descartes-szorzat R x R áll minden lehetséges valós számok. A pontok képviselő pár, teljesen kitölti a koordináta síkon. Így a Descartes-szorzat Rx R tartalmaz annyi elemek pontok találhatók a koordinátarendszerben.
A matematika és más tudományok tartják nemcsak a rendezett párok, hanem a rendezett sorozat három, négy, stb elemekkel. Például egy rekord számú 367 rendezett halmaza három elemből, és az írás a „matematika” - rendezett halmaza 10 elemekkel.
Megrendelt készletek gyakran nevezik sorok és hossza változó. tuple hossza - az elemek száma az azt alkotó. Például, (3, 6, 7) - egy tuple hossza 3 (m, A, T, F, m, A, T, és K, A) - egy tuple hosszúságú 10.
Fontolja meg a matek, és Descartes-szorzat három, négy, sőt készletek.
Definíció. Descartes-szorzat készletek A1. A2. A n a készlet minden szekvenciák n hosszúságú, amely tartozik az első sor A1 komponensként. második - A2 készlet. az n-edik - An set.
. Fe w n e elemek sokaságának A1 x A2 x A3 jelentése tuple hosszúságú 3 oly módon, hogy az első komponens az A1 tartozik a beállított, egy második - A2 készlet. harmadik - A3 készlet.