A divergencia vektor mező
Az áramlás az elektromos mező. Gauss-tétel integrál formájában
4. A divergencia a vektor mező. Gauss-tétel differenciális formában,
Tetszőleges vektor mezőben (azaz egy olyan vektorba funkciót. Az előre meghatározott pontokon (x, y, z) a régióban a tér) kapcsolatba hozható skalárfüggvény úgynevezett divergencia területén F. Ez a funkció jelöljük «div» és határozza meg a kapcsolatban
A divergencia fizikai jelentése a következő képlet bizonyított során magasabb matematika:
Ha a határérték mennyiségű V S és annak felülete koncentrációja a megfigyelési pont, ahol a divergencia számított. Szerint (1.4.1), a feszültség E áram bármilyen végtelenül kicsiny gömb, amelyen belül nincs díj - azonosan nulla. Ezért, (1.4.2), ebből következik, hogy a pontokat nulla töltéssűrűségű (r = 0) E divergencia eltűnik. Miután tekintve az áramlás a kis gömb pont körül V, ahol az eltérés a feszültség értéke nem nulla, akkor kimutatható használatával (1.4.1) és (1.4.2). hogy egy térbeli pontban felelős, ezért az a pont, ahol az eltérés feszültség nullától eltérő forrásai elektromos vezetékek.
A matematika képzés bizonyítani tétel Gauss-Ostrogradskii (hozta létre Gauss 1844-ben, függetlenül az MV Ostrogradskii bizonyította 1839-ben):
Itt V - tetszőleges határolt térfogaton felülete S. alkalmazni Tétel (1.4.3), hogy az áramlás a elektrosztatikus mező. Ami a (1.4.1), kapjuk:
A egyenlő a integrálok önkényes V térfogata miatt az egyenlő az integrandusok, azaz Gauss-tétel, differenciális formában (A. Poisson 1850 YG):
Azon régióinak hely, ahol E divergencia pozitív, az erővonalak árad E (r> 0), azokon a területeken, ahol a merülés <0 силовые линии заканчиваются (r<0), а через те области, где divE = 0 силовые линии проходят, но не рождаются и не исчезают, так как в этих областях r=0 (зарядов нет).
A cirkulációs rotor és a vektor mezőt. A gradiens egy skalár függvény
Circulation CL tetszőleges vektor mező F (x, y, z) határozza meg a következő összefüggés zárt áramkörben L:
ahol FI - vetülete a vektor irányát F áramköri elem dl (lásd 1.5.1 ..).
A rotor - ez egy másik koncepció a matematikai elmélete vektor területeken. Egy derékszögű koordináta-rendszer (x, y, z) F forgórész (kijelölése «ROTF») úgy definiáljuk, mint olyan vektor, amelynek az összetevői bizonyos kombinációi térbeli deriváltak a vektor F, nevezetesen:
Rotor fizikai jelentése következik az egyenlet azt bizonyította során matematika:
Ahol n - a normális, hogy a földre S, L - kontúr határoló a helyén, amely ebben az esetben a határérték szerződött a megfigyelési pont. Ha a rotor mezőt vektorba a megfigyelési pont nem egyenlő nullával, akkor bármilyen elegendően kis környezetében pontok területén vonalak képeznek mikroszkópos zárt hurok körül ( „örvény”). Ezért, a régió, ahol a vektor a területen rotor különbözik nullától, az úgynevezett örvény mező és a területen is, a rotort, amely a nullától különböző nevű örvény. A folyadék sebessége vagy gázáram, tekinthető koordináták függvényeként, egyértelmű példa egy vektor mező. Turbulencia a folyadék vagy gáz körül van kialakítva a pontok, ahol a forgórész nem nulla áramlási sebesség a folyadék (gáz). A képmezőt révén elektromos vezetékek a térben, ahol a forgórész nullától eltérő (ugyanúgy, mint a pont nem nulla divergencia), ez lehetetlen.
Mint később látni fogjuk, a keringés és a forgórész az elektrosztatikus mezők azonosan nulla az egész teret. Ezért az elektrosztatikus tér - viszonylag egyszerű erőtér. Ugyanezek a tulajdonságok és a gravitációs mező.
A koncepció a gradiens már bevezetett során a mechanika. Emlékezzünk rá. A gradiens az f (x, y, z), attól függ, hogy a koordinátákat - egy vektor, amelynek az összetevői a Descartes-féle térbeli deriváltak az f függvény:
Let. Tudjuk mutatni, hogy ha ez szükséges és elégséges, hogy a rotor nulla:
Potencialitását az elektrosztatikus mező. elektromos potenciál
A terepmunka a vizsgálati díj q transzfer pont 1 pont 2 nem függ a pályáját a mozgás és definiáljuk a területen, és a díjat csak a koordinátáit ezeket a pontokat. Olyan esetben, amikor a forrás mező egy pont Q töltésű (ábra. 1.6.1) ez könnyen igazolható az alábbiak szerint. A munka elemi szegmensben a röppálya, a jól ismert meghatározása mechanika, vagyis :. Bővülő skalár szorzata vektorok szögben egy közöttük, azt kapjuk,
Összefoglalva (integráló) minden elemi munka, azt látjuk,
QED. A munka határozza csak a távolság a forrástól a kezdeti és a végső pont a pálya. Egy ilyen erőtér mechanika hívtuk lehetséges.
A szuperpozíció elve kell lehetségesség elektrosztatikus mező által létrehozott díjak bármely rendszer. Tól (1.6.2) és a szuperpozíció elve azt is jelenti, hogy a munka az elektrosztatikus erők a töltést szállítanak el egy zárt körben egyenlő 0:
Ily módon minden egyes áramkör az elektrosztatikus térerő forgalomban - azonosan nulla. Összhangban az állítás (1.5.6) az elektrosztatikus térerősség (egy jel) lehet értelmezni, gradiens függvényében koordinátáit, az úgynevezett potenciális elektrosztatikus mezők:
A meghatározása elektrosztatikus mező intenzitás (1.2.1) és az összekötő között, az F erő képlet és a potenciális energia W, ismert mechanika természetesen
a (1.6.4), hogy a potenciális területen egy adott megfigyelési pont számszerűen egyenlő a potenciális energia egy teszt töltés q, helyezzük az adott pont, osztva a nagysága ezt a töltés:
A potenciális energia az elektrosztatikus mező, mint az energia a gravitációs térerő van meghatározva, akár egy tetszőleges konstans, amely lehet rögzített erre nullapont W. Általában, a potenciális energia egy elektrosztatikus mező nullával egyenlő a végtelenben.
Formula (1.6.4) integrálásával könnyen megkapjuk képlet kapcsolatos potenciális intenzitás:
Integráció (1.6.7) végezhetjük bármely összekötő görbe 1. és 2. pont.
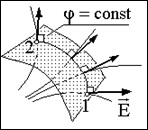
A hely, ahol van egy elektrosztatikus mező, mentális merőleges felület erővonalak. Kiszámításakor az integrál (1.6.7) 1-2 bármelyik mentén pályája, feküdt a felületre, a tangenciális komponens Et E jelentése nulla. Ezért, bármely két 1. és 2. pontjában a jobb oldali felület (1.6.7) nulla, a potenciálok j (r1) és j (r2) egyenlőek. A felület minden pontján, ahol a potenciális értéke azonos, az úgynevezett ekvipotenciális. Így, a felület merőleges a ekvipotenciális erővonalak.
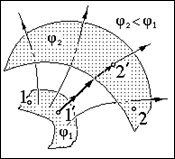
Általában a potenciális különbség 1 és 2 pont egyenlő a potenciális különbség az ekvipotenciális felületek tartozó, ezeket a pontokat. Az utóbbi megtalálható integrációt végrehajtó egyenlet (1.6.7) távvezetékek pontokat összekötő 1-es és 2 ¢ ¢ ezek ekvipotenciális felületek. Amikor ez valójában a szerves modulusa E az elektromos mező, mert A távvezeték. Összefoglalva tehát, egy pont Q töltésű területen potenciális adunk egy általános képletű, amely következik az összehasonlítás a képletek (1.6.2) és (1.6.6) és az ismert működési ütemének a mechanika közötti kapcsolat potenciális A12 erők a részecskék pályája rész 1-2, és a potenciális energia a részecskék kezdődő W1 és W2 végén ezt a részt:
Ebben az esetben, a részecske egy teszt q töltéssel. A képlet a potenciális pont távol pontszerű forrásból Q a távolság r. úgy néz ki,
Az elektromos mező - egy adott formáját mezőt, hogy létezik körül a szervek vagy részecskéket, amelyek elektromos töltés, valamint a szabad formában elektromágneses hullámokat. Az elektromos mező közvetlenül látható, de meg lehet figyelni a hatást és a segítségével eszközöket. A fő hatása az elektromos mező a gyorsulás a szervek vagy részecskék elektromos töltést.
Az elektromos mező lehet tekinteni, mint egy matematikai modell, amely leírja az érték az elektromos tér egy adott pontján az űrben. Duglas Dzhankoli írta: „Hangsúlyozni kell, hogy a tér nem valamiféle anyag, inkább egy rendkívül hasznos fogalom ... A kérdés az” valóság „és az, hogy az elektromos mező valójában - egy filozófiai, sőt metafizikai kérdés a fizika megértését. mező bizonyult rendkívül hasznos - ez az egyik legnagyobb vívmánya az emberi elme. "
Az elektromos mező komponense az elektromágneses mező és egy megnyilvánulása az elektromágneses kölcsönhatás.
Irodalom
Az áramlás az elektromos mező. Gauss-tétel integrál formájában
Információk a „térerősség”
Kategória: Fizika
Karakterek száma szóközökkel: 24053
Asztalok száma: 1
Képek száma: 7
jelenlegi két változó: a polarizáció és az esetleges változás sebességét. Ez a megközelítés lehetővé teszi a modellezést tranziens elektromos mezőt elektrokémiai rendszerekben. A matematikai modell tekinthető töltve vezető közegben a D-szakaszban, ahol S határa áll az anód Sa, katód Sk és Si elszigetelt helyek: S = Sa # 61.525; Sc # 61.525; Si, = D # 61.525; S, függőség.
kétszer. A tapasztalat azt mutatja, hogy a kölcsönhatás erő megfeleződik. Visszhangos hasonló technikával, biztos lehet benne, hogy a teljesítmény arányos a termék a díjakat. Mivel az elektromos mező kölcsönhatása két díj? Eredetileg úgy hitték, hogy a díjak közvetlenül az egész semmis aktus egymásra. Minden díj a távolból „érzi” a másik jelenléte. Ez így volt.
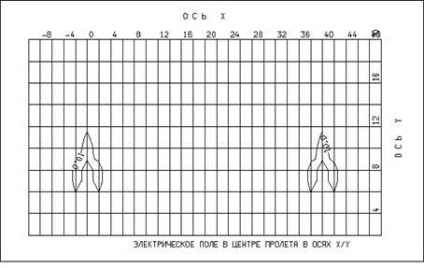
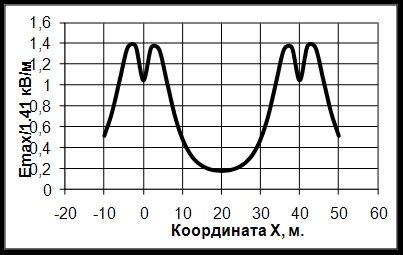
annak végrehajtását. 1. Adagolási elektromos mezők jelen nemzetközi szinten, és számos fejlett országban, köztük saját, kidolgozott és elfogadott dokumentumok szintjét szabályozza elektromos mezők által generált magas feszültségű készülékek és berendezések. Először a szabványok az elektromágneses mezők kerültek meghatározott [1, 2, 3, 4, 5]. Magyarországon szabályozzák.
részvétele a negatív ionok a folyamat lassú oxidáció. Összegezve az összes fenti, meg kell jegyezni, hogy a két fő szempont a hatásmechanizmusa az elektromos mező az égési folyamat (befolyásolja a gáz dinamikáját a folyamat vagy közvetlen hatással a reakció kinetika) tükrözi a két általánosabb fogalmakat illetően szerepe és helye a töltött részecskék az égési folyamat, egy.