1) A probléma a lineáris programozás, és különböző formái a bejegyzéseket

Optimalizálás és matematikai módszerek a döntéshozatal

Ha a célfüggvény és a rendszer lineáris korlátokat. A matematikai programozási feladat az úgynevezett lineáris programozás feladata (ZLP).

Az alapvető formája a ZLP

Szimmetrikus forma ZLP

Általános lineáris programozási feladat

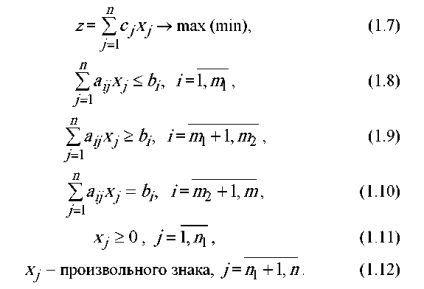
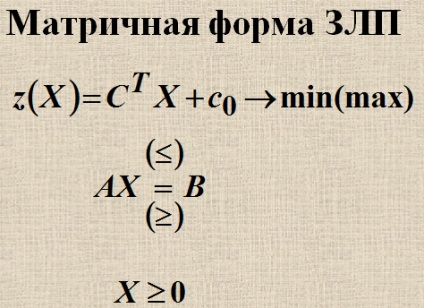
Bármilyen lineáris programozási probléma csökken a standard (kanonikus) képezik a fő lineáris programozási probléma, amelyet az alábbiak szerint történik: találni egy nem-negatív változók X1, X2, Xn, kielégíti a korlátok formájában egyenletek:

A11X1 + A12X2 + ... + A1nXn = B1;

A21X1 + A22X2 + ... + A2nXn = B2;

Am1X1 + Am2X2 + ... + AmnXn = Bm;

és utal a maximális lineáris függvénye ezeket a változókat:

E = C1X1 + C2X2 + ... + CnXn Þ max

Arra is szükség van, hogy a jobb oldalán nemnegatív, vagyis feltételeknek kell teljesülniük:

Csökkentés formanyomtatvány van szükség, mert a legtöbb megoldási módjait, lineáris programozási feladatok fejlesztik, csak a szokásos formában. Hogy a szokásos formáját a lineáris programozási feladat lehet, hogy hajtsa végre a következő lépéseket:

mozgatni a minimalizálás a célfüggvény maximalizálása azt;

megváltoztatni a jelei a jobb oldalán korlátozások;

megy-egyenlőtlenség korlátokat egyenlőséget;

megszabadulni a változók, amelyek nem korlátozzák a jel.

Hogy oldja meg a problémát, akkor használja a szimplex módszer, mivel ez a módszer megoldására lineáris programozási feladatok minden dimenzióban.

2) csökkentése az általános probléma a LP a kanonikus formában.

Bármely lineáris programozási feladat lehet csökkenteni a lineáris programozási feladat kanonikus formában. Erre a célra általában azt kell, hogy képes csökkenteni a maximalizációt minimalizálása a problémát; áttérés egyenlőtlenség korlátokat egyenlőség korlátok, és cserélje ki a változókat, amelyek nem tartoznak a nem-negatív állapot. Maximalizálása egy függvény egyenértékű minimalizálása ugyanazt a funkciót, hozott ellenkező előjelűek, és fordítva.

Általában hozza lineáris programozási feladat kanonikus formában a következő:

ha az eredeti probléma az, hogy meghatározza a maximális lineáris függvény, meg kell változtatni a jel, és keresse meg a minimum ezt a funkciót;

ha korlátozásokat a jobb oldalon negatív, meg kell szorozni -1 ezt a határt;

ha bizonyos korlátozások vannak az egyenlőtlenség, akkor bevezetésével további nem-negatív változók alakítjuk tőke;

1. példa Reduction a kanonikus forma lineáris programozási probléma:

Perc L = 2x1 + x2 - X3; 2x2 - X3 ≤ 5; x1 + x2 - X3 ≥ -1; 2x1 - x2 ≤ -3; x1 ≤ 0; x2 ≥ 0; X3 ≥ 0.

Bemutatjuk az egyes egyenlet korlátozások szintező rendszer változók x4, x5, x6. A rendszer formáját ölti egyenletek, amelyek szerepelnek a bal oldali első és a harmadik egyenlet a rendszer korlátai változók x4, x6 egy „+”, a második egyenlet változó x5 szerepel a „-” jel.

Ingyenes tagok kanonikus formában pozitívnak kell lennie, mert ez az utolsó két egyenlet, szoroztunk -1:

Behelyettesítve ezt a kifejezést a rendszer korlátai, és a célfüggvény és írásban változók növekvő sorrendben az index, megkapjuk a lineáris programozási bemutatott kanonikus formában:

3) A feltétel optimalitása az alap terv a kanonikus LP problémát. Szimplex módszer és a konvergencia.

A szimplex módszer univerzális, mivel lehetővé teszi, hogy megoldja szinte minden problémát a lineáris programozás, rögzítik a kanonikus formában. Az az elképzelés, a szimplex a szimplex módszer az a tény, hogy, kezdve néhány kezdeti összehasonlító oldatok, végezzük egymást követően irányított mozgását az alátámasztó optimális megoldást a problémára. Az érték a célfüggvény mozgás közben maximális problémák nem csökken.

Mivel a több összehasonlító oldatok természetesen véges számú lépésben megkapjuk az optimális támogatási megoldás. Az összehasonlító oldat nevezzük alap, nem-negatív oldatban.

szimplex módszer algoritmus 1. A matematikai modellje a probléma, hogy a kanonikus. Ha ez nem kanonikus, akkor csökkenteni kell a kanonikus formában. 2. Keresse meg az eredeti összehasonlító oldat és tesztelje optimalitást. Hogy töltse ki ezt simplex 1. táblázatban az összes sort a táblázat 1. lépés szerinti töltőanyag rendszer korlátai, és az objektív függvény.

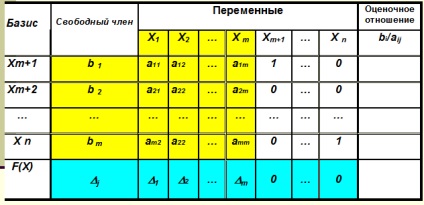
Az alábbi esetekben a problémák megoldásában, a maximum:

1. Ha az összes együtthatóit az utolsó sor a szimplex táblázat j 0, akkor talált

2 Ha legalább egy együttható j 0, de a megfelelő változó nem egyetlen pozitív értékelést kapcsolat, akkor a megoldás megálló, Mivel az F (X) , t.e.tselevaya funkció nem korlátozódik a terület megvalósítható megoldásokat.

Ha legalább az egyik utolsó sorban együttható negatív, és ha a megfelelő változót legalább egy becsült értékeinek pozitív hozzáállás. akkor meg kell pereytik másik összehasonlító oldat.

4. Ha a negatív tényezők az utolsó sor száma adja meg a változó bazisnoyperemennoy (PD) oszlopban. amely megfelel a legnagyobb abszolút velichineotritsatelny együttható.

5. Ha legalább egy koeffitsientk <0 ,то k- тый столбец принимаем за ведущий.

6. A vezető húr fogadja az egyik, hogy megfelel a minimális aránya a szabad tagok bi pozitív tényező, ami, k az oszlop.

7. Egy elem elhelyezkedik peresecheniiveduschih sor és oszlop nazyvaetsyaveduschim elem.

Töltsük simplex 2. táblázat:

 az alap feltöltéséhez oszlopot nullák és egyesek

 átírni a vezető vonal, osztja azt a vezető elem

 ha a vezető sor nulla, akkor a következő szimplex táblázatot át lehet vinni a megfelelő oszlopok

 megtalálják a maradék együtthatók szerint a „téglalap”

Kapunk egy új referencia megoldás, amely ellenőrzi optimalitást:

Ha minden együttható az utolsó sor j 0, a talált megoldás a maximális.

Ha nem, töltse ki a szimplex tábla 8. lépést, és így tovább.

Ha a célfüggvény F (X) igényel megtalálni a minimális érték. optimalitásával kritériuma a probléma nem pozitív együtthatók jpri vsehj = 1,2.n.

A konvergencia a szimplex módszer. Degenerációja LP problémát. A legfontosabb tulajdonsága a számítógépezés, a konvergencia az algoritmus, azaz a. E. Az a lehetőség, annak alkalmazása a kívánt eredményt (pontosan egy előre meghatározott, Stu) véges számú lépésben (iteráció).

Könnyen megjegyezni, hogy problémák konvergencia simplex IU-Toda potenciálisan előfordulhat határozat r értéket (p. 2 „) abban az esetben, ha a minimális érték azonos viselő

Ők fogják elérni több sor a táblázat T (q) egyidejűleg-Menno. Majd a következő iterációban B oszlop (β (q + 1)) fogja tartani a CO-nulla elemek.

Kapcsolódó cikkek

• Szimplex módszer megoldására lineáris programozási feladatok 1

• Lineáris programozási feladat

• A kanonikus alakja lineáris programozási feladat