Bemutatás a parabola témájáról és annak alkalmazásáról a szerző, a chekureeva love, a 9-a-osztályú diák
2 A projekt célja. a második sor (parabola) egyik görbületének tanulmányozása és alkalmazásának szférája. A projekt célkitűzései. 1. Adjon szigorú matematikai definíciót egy parabola számára. 2. Tanulmányozza a parabola tulajdonságait. 3. Tájékozódjon arról, miért nevezzük a parabolát kúpszeletnek. 4. Határozza meg a parabola alkalmazását.

Parabola 3 (Gk. Παραβολή alkalmazás) görbe, melynek pont egyenlő távolságra van egy pont, úgynevezett fókusz, és egy egyenes vonal, az úgynevezett direktrixét egy parabola. Az ellipszis és a hiperbola mellett a parabola kúpszelet. A kúp alakú kép, amely egy parabola. Parabola mint kúp alakú építése.

4 Miért kell egy parabolát kúpszeletnek nevezni? A parabola egy kúp egy része a generátrixával párhuzamos síkban.

5 Parabola felépítése Az első módszer. Parabola, akkor egy „pontról pontra” egy uralkodó és iránytű, anélkül, hogy tudnánk az egyenletet, amelynek jelenlétét csak a fókusz és az direktrix. A csúcs a szegmens középpontja a fókusz és a rendező között. A direktrixon megadható egy tetszőleges referenciakeret a kívánt egységintervallummal. Minden egyes egymást követő pont metszi a merőleges szegmens közötti fókuszpont és a direktrix, található többegységes intervallumban távolságra a vonatkozási pont, és az egyenes, amely áthalad a pont és tengelyével párhuzamosan a parabola
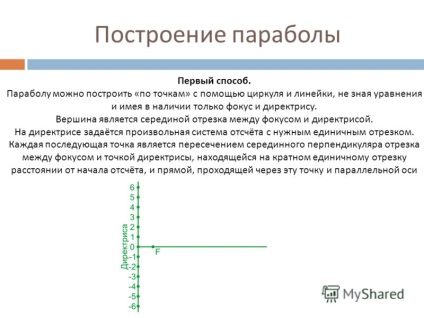
6 Parabola építés A második út. Annak érdekében, hogy rajzoljon egy parabolát, szükséged lesz egy vonalzóra, egy négyzetre, egy szál hosszúságára, amely megegyezik a négyzet nagyobbik lábával és a gombokkal. Csatlakoztassa a fonal egyik végét a fókuszba, a másik pedig a négyzet kisebb sarkának csúcsához. Az uralkodót alkalmazza az igazgatóra, és helyezze a négyzetet egy kisebb lábra. Egy ceruzával húzzuk meg a szálat úgy, hogy annak pontja megérinti a papírt, és egy nagyobb lábra nyomja. Mozgatjuk a négyzetet, és a ceruzát a hasáb felé nyomjuk, hogy a szál kifeszítve maradjon. Ebben az esetben a ceruza rajzol a parabola a papíron.

7 Parabola tulajdonságai 1. A parabola a második sor görbéje. 2. A szimmetria tengelye a parabola tengelye. A tengely áthalad a fókuszon és a csúcs merőleges a rendezőre. 3. Optikai tulajdonság. Egy parabola tengelyével párhuzamos sugarak sugara, melyet parabola tükröz, összpontosul. Ezzel szemben a fókuszban lévő forrás fényét egy parabola tükrözi a tengelyével párhuzamos sugárnyalábba. 4. A parabola esetében a fókusz a ponton (0; 0,25). Egy parabola esetében a fókusz a (0; f) ponton van. 5. Minden parabola hasonló. A fókusz és a rendező közötti távolság határozza meg a skála méretét. 6. Ahogy a parabola a szimmetria tengely körül forog, egy elliptikus paraboloidot kapunk.

8 Parabolikus tulajdonságok A Pn-től az F középpontig terjedő távolság megegyezik a Pn-Qn értékével. Illusztráció Pascal tételének bizonyítására a tételen keresztül 9 ponton. Az F-Pn-Qn vonalak hossza ugyanaz. Elmondhatjuk, hogy az ellipszisektől eltérően a második fókusz a parabola végtelenben van (lásd még Dandelen golyók).

9 Paraboloidok A paraboloid egy parabola mozgásával jön létre, amelynek csúcsa egy másik helyhez kötött parabola mentén csúszik. Ebben az esetben egy elliptikus és hiperbolikus paraboloidot kapunk. Elliptikus paraboloid. Hiperbolikus paraboloid.

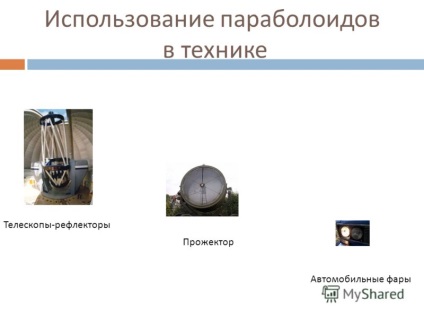
10 A paraboloidok használata a technikában A forradalmi paraboloid egy fókuszpályával párhuzamos sugárnyalábot egy pontra fókuszál. Gyakran használják a forradalmi paraboloid tulajdonságait, hogy egy fókuszponttal párhuzamos sugárnyalábot gyűjtsön egy fókuszpontba, vagy fordítva, hogy egy sugárzás párhuzamos sugara legyen a fókuszban található forrásból. Ez az elv parabolikus antennákon, teleszkópokon - fényvisszaverőkön, fényszórókon, autólámpákon alapul. Rádiótávcső antenna.
11 Paraboloidok használata a technikában Teleszkópok - reflektorok Searchlight Automotive fények
12 Solar Lighter Az eredeti energiafelhasználás módja. A szoláris öngyújtó parabolikus rozsdamentes acél tükör, amely majdnem ugyanaz, mint az athéni olimpiai láng meggyújtása. A parabola tükör lehetővé teszi, hogy összegyűjtsék az összes energiát egy fókuszpontban és tüzet gyújtsanak. A hőmérséklet ezen a ponton elérheti az 537 Celsius fokot. Az ilyen eszköz nélkülözhetetlen a kampányban és más terepi körülmények között.
13 Parabolák a fizikai térben A Leonardo da Vinci parabolikus iránytűje. A parabola pályája és a műhold mozgása mentén.

14 parabolák a fizikai térben pályáira kozmikus testek (üstökösök, kisbolygók és egyéb), halad közel csillagok vagy más nagy tömegű objektumok (csillagok, fekete lyukak, vagy csak a világon) kellően nagy sebességgel formájában vannak a parabola (vagy túlzás). Ezek test miatt a nagy sebesség és a kis tömeg, ne szoruljanak a gravitációs mező a csillag, és továbbra is ingyenes járat. Ezt a jelenséget használják az űrhajók gravitációs manővereihez.
15 Parabolák a fizikai térben A kosár kosárja. Parabolikus napenergia-erőmű Kaliforniában, USA.
16 Kaluga, Kultúra és Szabadidőpark Parabola a fizikai térben A vízsugarak pályái
17 Parabolák Kaluga fizikai térben, Győzelmi tér Vízsugarak pályái
18 A parabola alkalmazása ballisztikus ballisztikában (a görög βάλλειν dobástól) a matematika és a fizika alapján az űrben elhagyott testek mozgásának tudománya. Elsősorban a lőfegyverekből, rakétákból és ballisztikus rakétákból lőtt lövedékek mozgásának kutatásában vesz részt. Vannak belső ballisztikák, amelyek a lövedék mozgását vizsgálják a pisztoly csatornájában, szemben a külső ballisztikával, amely megvizsgálja a lövedék mozgását, amikor kilép a pisztolyból. A külső ballisztika szerint általában a testek mozgásban való tudományát értik a levegőben és a levegő nélküli térben, csak külső erők hatása alatt.
19 Parabolák az állatvilágban Az állatok ugrásának pályái közel vannak a parabolához
20 Parabolák az állatvilágban Az állatok ugrásának pályái közel vannak a parabolahoz
21 Parabolák az állatvilágban Az állatok ugrásának pályái közel vannak a parabolahoz
22 Parabolák az építészetben
23 Függesztő híd A szerkezet szerkezete. A felfüggesztett híd fő feszültségei a fő kábelek húzófeszültségei és a támasztékok nyomófeszültségei, a feszültségek nagyon kicsiek. A tartók szinte minden ereje függőlegesen lefelé irányul és a kábelek miatt stabilizálódik, ezért a támaszok nagyon vékonyak lehetnek. A különböző szerkezeti elemek közötti viszonylag egyszerű terheléseloszlás egyszerűsíti a szuszpenziós hidak kiszámítását. A híd súlyának és tömegének hatása alatt a kábelek a parabola közelében ívek és ív alakulnak ki. A két tartó között felfüggesztett, terheletlen kábel az ún. A "láncvonal", amely közel áll a parabolahoz, szinte vízszintes szakaszban. Ha a kábelek súlya elhanyagolható, és az oszlop súlya egyenletesen eloszlik a híd hossza mentén, akkor a kábelek parabola formájúak. Ha a kötél tömege összehasonlítható az úttest tömegével, alakja a láncvonal és a parabola közötti lesz.
26 Összefoglalás A projekt munkája során. 1. Egy parabola szigorú matematikai meghatározását megfogalmazzuk. 2. Megfontolandó a parabola felépítésének módja. 3. A parabola néhány tulajdonságát tanulmányozzák. 4. Megállapították a "parabola" és a "kúpos szakaszok" fogalmának kapcsolatát. 5. A parabola alkalmazási területeit meghatározzák (fizika, mérnöki, ballisztikai, csillagászati, építészeti, hídépítés). 6. Megerősítettük a matematika fontosságát a körülöttünk lévő világban.
27 Internet - források parabola antenna kúpszeletek Reflektor _ (teleszkóp) Reflektorfény _ (fizika) függőhíd elliptikus paraboloid