A hibaarány kiszámítása
Az első hiba előtti tételben a termékfejlesztés átlagos értéke az első hiba előtt az átlagos működési időnek nevezzük. Ez a kifejezés mind az javítható, mind a nem javított tárgyakra vonatkozik. A nem javítható termékek esetében a név helyett a meghibásodás időtartamát lehet használni.
A GOST 13377 - 67 a nem megerősített termékekhez újabb megbízhatósági mutatót vezetett be, amelyet meghibásodási aránynak neveztek.
A meghibásodási intenzitás annak a valószínűsége, hogy egy felmondhatatlan termék, amely hibátlanul működött mindaddig, amíg a pillanat t nem, egy későbbi időegységben meghiúsul, ha ez az egység kicsi.
A termék meghibásodási sebessége a mûködésétõl függõ idõ függvénye.
- számítsuk ki a λ (t) hibaarányt t és Δt megadott értékekre.
- feltételezve, hogy a megbízhatóság egy egység az autó elektronikus vezérlés jellemzi hibaszázalékkal számszerűleg egyenlő a számított, és ez az intenzitás nem változik élettartama alatt meg kell határozni az idő, hogy tény, hogy a TB egységet.
A vezérlő alrendszer tartalmaz k-sorozathoz csatlakoztatott elektronikus egységeket (2.
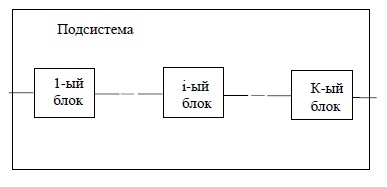
2. ábra Ellenőrző alrendszer egymást követő blokkokkal.
Ezek az egységek azonos hibaszázalék számított számszerűen egyenlő. Szükséges, hogy meghatározzuk a hibaszázalék Xp alrendszer és az átlagos időt, amíg hiba, építeni szerinti a valószínűsége, hibamentes működés az egyik RB egység (t) és RP alrendszer (t) a működési idő, és meghatározza a valószínűsége hibamentes működés RB egység (t) és RP alrendszer (t), hogy a működési idő t = TP.
A hibaarány λ (t) a következő képlet segítségével számítható ki:
Hol található a [t, t + Δt] intervallumon belüli eszköz meghibásodásának statisztikai valószínűsége vagy egyébként a T valószínűségi változó statisztikai valószínűsége a meghatározott időközönként.
P (t) az 1. lépésben kiszámított eszköz kudarcmentes működésének valószínűsége.
Műszaki adatok 10 3 h - 6,5
A [t, t + Δt] intervallum [6,5 * 10 3 h, 9,5 * 10 3 h]
λ (t) = 0,4 / 0,4 * 3 * 10 3 h = 0,00033
Tegyük fel, hogy a hibaarány nem változik az objektum teljes élettartama alatt, azaz λ (t) = λ = const, akkor a hiba mûködési ideje egy exponenciális (exponenciális) törvény szerint oszlik meg.
Ebben az esetben az egység hibás működésének valószínűsége:
RB (t) = exp (-0,00033 * 6,5 * 10 3) = exp (-2,1666) = 0,1146
És az egység átlagos működési ideje a következő:
= 1 / 0,00033 = 3030,30 óra.
A k blokkok egymás utáni összekapcsolásával az általuk létrehozott alrendszer hibaszázenseje:
Mivel az összes blokk hibája erőssége megegyezik, az alrendszer hibáinak intenzitása:
λP = 4 * 0.00033 = 0.00132 h.
és a rendszer hibás működésének valószínűsége:
RP (t) = exp (-0,00132 * 6,5 * 10 3) = exp (-8,58) = 0,000188
Figyelembe véve a (7) és (8) pontokat, az alrendszer átlagos működési ideje a következő:
= 1 / 0.00132 = 757,58 rész.
Következtetés: amikor megközelítjük a határállapotot, megnő az objektumhibák intenzitása.
A hibamentes működés valószínűségének kiszámítása.
Feladat: A t = kiszámításához a Pc () rendszer hibás működésének valószínűségét (3. ábra) kell kiszámítani, amely két alrendszerből áll, amelyek közül az egyik a tartalék.
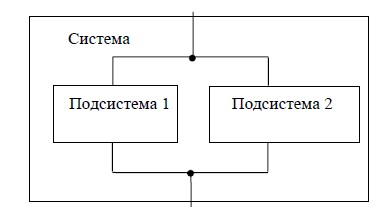
Ábra. 3 Rendszerdiagram redundanciával.
A kalkuláció azon a feltételezésen alapul, hogy a két alrendszer hibái függetlenek.
Az egyes rendszerek hibamentes működésének valószínűsége megegyezik és RP () egyenlő. Aztán az egyik alrendszer meghibásodásának valószínűsége:
QP () = 1 - 0,000188 = 0,99812
Az egész rendszer meghibásodásának valószínűségét az állapítja meg, hogy az első és a második alrendszer hibás, azaz:
= 0,99812 2 = 0,99962
Ezért a rendszer hibás működésének valószínűsége:
,
Pc () = 1 - 0,98 = 0,0037
Következtetés: ebben a feladatban a rendszer hibamentes működésének valószínűségét az első és a második alrendszer hibájára számítottuk ki. A szekvenciális szerkezettel összehasonlítva a rendszer hibás működésének valószínűsége kisebb.