A helyi görbék szinuszosak, spirálok és görbék, egyenletekkel kifejezve, rajzok az iskolások számára
Szinuszos. Egy sík görbe, amely a szög nagyságának a szög nagyságának függvényében történő változását jellemzi, szinuszosnak nevezzük. Egy szinuszos eszköz létrehozásához az adott kör több egyenlő részre oszlik (1. Ugyanazon számú egyenlő részre osztja a szinuszos tengelyt, amelynek hossza megegyezik a 2nR kör hosszával. A felosztási pontoktól merőlegesek a tengelyre húzódnak, amelyen az ordinátákat lefektetik, egyenlőnek a szinusz megfelelő szegmenseivel. A kapott I., II., III. Stb. Pontokat sima görbe kapcsolja. Szükség esetén a görbe a VIII. Ponton túl is folytatható. A technika gyakran előforduló csavarjainak kialakítása során egy sűrített szinuszot használnak, amelynél a perem kisebb, mint a kerülete.
Ábra. 1. Szinuszos szerkezet kialakítása
Spirál. Egy síkgörbe, amelyet egy bizonyos központ köré forgó pont mozgatásával nyerünk, és egy bizonyos törvénynek megfelelően egy időben elmozdulunk is, spirálisnak nevezzük. Ha a középponttól való távolság arányos a pont szögeltérésével, akkor a görbét Archimedes spirálnak nevezik. A görbe méretei függenek az OVIII spirál magasságának nagyságától (2. ábra). A görbe megépítéséhez húzzon egy olyan kört, amelynek sugara egyenlő a spirális pályán. Oszd meg a lépést és a kört azonos számú egyenlő részekkel. Az O középpontból egy, kettő, három stb. Rész van elhelyezve a sugár mentén, az I, II, III spirál stb.
Az egyenletek által kifejezett görbék. A rendszeres görbéket gyakran egyenletekkel adják meg. Tegyük fel például, hogy létre kell hoznunk az x = y2 + 2 egyenlet által adott görbét (3. ábra). Az x és y koordináta tengelyek húzódnak. Helyettesíti az egyenletben a mennyiség helyett: 0, 1, 2, 3, 4 stb. Mekkora az x értéke ebben az esetben. Az előbbi esetben, x = 2, a második az x = 3, a harmadik - b, a negyedik - .. 11, stb ábrázolva x és y tengely a megfelelő mennyiségben és a kereszteződésekben a merőlegesek olyan pontok I, II, III, IV, V és mások.
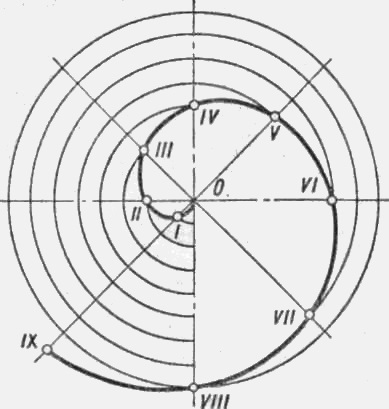
Ábra. 2. Archimedes spirál építése
Ábra. 3. A görbe építése egyenértékből.