Gradiens tulajdonságok
Definíció 3. A függvény egy gradiens egy ponton olyan vektor, amelynek koordinátái a standard alapon vannak. Rövidebb gradiens kijelölés (az ikon olvasható "nabla").
Fogalommeghatározás 4. Let. A Yak mátrixóEnnek a leképezésnek egy pontja egy mátrix, amely minden egyes koordinátában az egyes komponensek származékait tartalmazza. A vektorra vonatkozó származékot ugyanúgy definiáljuk, mint korábban.
Definíció 5. A leképezés egy ponton differenciálhatónak nevezhető, ha annak teljes növekménye formában megjeleníthető
, ahol egy lineáris operátor, vagyis egy térkép, amely rendelkezik a linearitási tulajdonsággal:. Az üzemeltető térben és térben működik. Ezt a származtatott leképezésnek nevezik és jelölik. A kifejezést vagy különbségnek nevezzük, és jelöljük. Nyilvánvaló, hogy a folytonosság a különbségtételből következik.
1. tétel (a különbségtételhez szükséges feltétel). Ha a leképezés egy ponton differenciálható, akkor ezen a ponton minden részleges származék és akár származék származik minden vektor vonatkozásában. Ebben az esetben. Azonban, ellentétben az egyik változó funkciójával, egy származék létezése bármely vektorra vonatkozóan nem jelenti a leképezés különbözőségét.
Bizonyítás. Hadd legyen. majd
Ezért. Az inverz következtetés hiánya például a következő ellenpélda alapján látható.
Ellenpélda. Hadd legyen. Ez a függvény származtatott egy vektor bármely pontján, és ez a származék egyenlő. Ha a függvény egy ponton differenciálható, akkor a kifejezés lineárisan függ a vektortól. Ez lenne az. Azonban nem mindig. Például, vagy.
Következmény. Ha a térkép egy ponton differenciálható, akkor ezen a ponton minden részleges származék létezik, és egy lineáris mátrix
a standard alapon a Jacobi mátrix.
* Bizonyítás. A mátrixelemeket a bázison jelöljük. Akkor lesz.
Tétel: 2. (A különbözőséghez elegendő feltétel). Ha minden részleges származék egy pont szomszédságában létezik és folyamatosan a ponton van, akkor a térkép ettől kezdve megkülönböztethető.
Bizonyítás. A feltüntetett körülmények között elegendő a skaláris függvény különbségének bizonyítása, vagyis a leképezés egyik összetevője. A bizonyítási módszer könnyebb megérteni a. Van
, ahol a szám a számok között van, de a számok között van (Lagrange tétele).
Ha nullára hajlamosak, akkor szintén nulla. A származékok folyamatosságát a ponton kapjuk. H, stb.
1 о. Vegyünk egy skaláris mezőt, azaz egy függvényt. Ha az f függvény egy ponton differenciálható, akkor, mint már tudjuk,. A mi esetünkben ez azt jelenti
Mivel egy vektor irányú kosinjei egyenlők, az egységhossz vektora. Megkapjuk az irányszármazék számításának képletét:
A Cauchy egyenlőtlenség ezt mutatja. Az egyenlőség csak akkor lehetséges, ha a vektorok kollineárisak. Így az irányszármazék a legnagyobb értéket veszi fel, ha a vektorral kollineáris. Ez a legnagyobb érték is. Ebből következik, hogy egy gradiens új (koordinátamentes) definíciót adhat.
Definíció. A függvény egy gradiens egy ponton olyan vektor, amelynek hossza megegyezik a legnagyobb származékokkal egy adott pont mentén. A gradiens iránya egybeesik a funkció leggyorsabb növekedésének irányával.
Látjuk, hogy a skaláris mező gradiense (egy függvény) nem függ a koordináták választásától, hanem maga a mező határozza meg.
Megjegyezzük, hogy a "mínusz gradiens" irányba a funkció leggyorsabban csökken, és a gradiensre merőleges irányban a funkció nullázza a változást, mert akkor, ha igen.
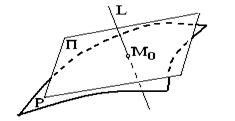
2 о. Egy implicit egyenlet által definiált felületet tekintünk, ahol az ezen a felületen elhelyezkedő ponton megkülönböztethető, és a gradiens ekkor nem nulla (ilyen pont rendszeresnek nevezik). Az ezen a ponton átmenő és a vektorra merőleges egyenes vonalak egy síkban helyezkednek el, amelyet a ponton lévő érintő síknak neveznek. Az érintő sík egyenlete formában van
Azt is megadjuk a normális (vagyis a síkra merőleges és a ponton áthaladó vonalat) kanonikus egyenleteit:
Hagyja, hogy a felület egyenlete egy explicit formává redukáljon, ahol a függvény egy ponton differenciálható. Ha elfogadja, akkor ismét visszatérünk az egyenlethez. Ezért tehát az érintő sík egyenlete a forma
ahol (hasonlítsa össze a gráf érintőjének egyenletét).
Világos, hogy mikor. Így a pont szomszédságában lévő érintő sík közelebb van a felülethez, mint bármely más sík.
A normál egyenletek most már formát öltenek
Egy példa. Írja le az érintő sík és a normális egyenleteit az ellipszoidra egy ponton.
A megoldás. Először is, egy adott felülethez tartozik, mert .
1. módszer. mert , akkor. Feltételezzük, hogy az érintő sík normálvektorja megegyezik.
Ezért megkapjuk az egyenleteket és.
2. módszer. . Következésképpen ,,,. Ezért az érintő sík egyenlete az alábbi alakú: vagy, és a normális kanonikus egyenleteivel:.
Exercise. Bizonyítsuk be, hogy az érintő sík egyenlete egy ellipszoidhoz, az egyenlethez egy olyan ponton, amely ezen a felületen fekszik.
Oldal generálása: 0.008 mp.