Fizika könyv 1
1. Adja meg a meghatározást: a) a relatív hosszirányú deformáció, b) a relatív keresztirányú deformáció. Adja meg a megfelelő matematikai kifejezéseket, bővítse ki a benne foglalt mennyiségek fizikai jelentését. Adja meg a mértékegységeket.
2. Adjon meghatározásokat: a) normál mechanikai feszültség, b) tangenciális (tangenciális) stressz. Adja meg a megfelelő matematikai kifejezéseket, bővítse ki a benne foglalt mennyiségek fizikai jelentését. Adja meg a mértékegységeket.
3. Adja meg a meghatározást: a) az elasztikus kompressziós-expanziós törzs törvénye, b) a rugalmas nyíróer-deformáció törvénye. Adja meg a megfelelő matematikai kifejezéseket, bővítse ki a benne foglalt mennyiségek fizikai jelentését.
4. Határozza meg az anyag rugalmassági modulusa E. Bővítse fizikai jelentését, adja meg a mérési egységeket.
5. Sorolja fel a deformációk főbb típusait. Amit a legegyszerűbb fajták csökkenthetők.
6. Mi a különbség a rugalmas deformáció és a műanyag deformáció között?
7. Mi a nagy rugalmasságú deformáció jellemzője? Milyen testek vannak?
8. Adja meg az erő pillanatának meghatározását, adja meg a megfelelő matematikai kifejezéseket, bővítse ki a benne foglalt változók fizikai jelentését, adja meg a mérési egységeket.
9. Írja le a forgó tengelyhez tartozó test egyensúlyi állapotát.
10. Adja meg a Poisson arányát. Adja meg a megfelelőt
matematikai kifejezés, megnyitja a benne foglalt mennyiségek fizikai jelentését.
Adja meg a mértékegységeket.
11. Adja meg az anyag szilárdságának meghatározását. Írja le az erő alapvető feltételeit.
12. Mi a különbség a technikai és elméleti erősségek között? Melyik közülük
többet és miért?
13. Sorolja fel az anyagok megsemmisítésének fő típusát. Hogyan különböznek egymástól?
14. Az "energetikai szempontból" megfogalmazza a mikrotörések csírázásának állapotát.
Magyarázatok a megfelelő ütemterv segítségével.
15. Milyen alapvető mechanikai tulajdonságokat lehet meghatározni a diagramból?
16. Adja meg az anyag keménységének fogalmát. Sorolja fel a meghatározás fő módszereit, adja meg a megfelelő matematikai kifejezéseket, nyissa meg a benne foglalt mennyiségek fizikai jelentését. Adja meg a mértékegységeket.
17. Hogyan viszonyulnak az anyag fő mechanikai jellemzői: a Young modulus, a nyírási modulus és a Poisson aránya. Adjunk megfelelő matematikai kifejezést, nyissuk meg a benne foglalt mennyiségek fizikai jelentését.
18. Mi az anyag tartóssága, mit mérünk? Hogyan függ az anyag tartóssága az alkalmazott mechanikai feszültségtől? Adjunk megfelelő matematikai kifejezést, nyissuk meg a benne foglalt mennyiségek fizikai jelentését.
19. Hogyan változik az anyag tartóssága a hőmérséklet függvényében? Adja meg a megfelelőt
matematikai kifejezés, megnyitja a benne foglalt mennyiségek fizikai jelentését.
20. Mi a fizikai jelentése a "Txp törékenység hőmérséklete"
21. Az "orthosilium-M" minta - az L0 = 20 mm kezdeti hosszúságú szilikonalapú bélések anyagát egy relatív deformációval feszítik ki ε = 1,5. Határozzuk meg a kapott minta hosszát L.
22. Minta "ortoszil-M" - alapanyagú szilikon alapágyakhoz
L0 = 20 mm L = 40 mm hosszúságig húzódik. Határozzuk meg az ε minta relatív deformációjának értékét.
23. Az "orthosilium-M" mintát - a szilikon alapú bélések anyagát egy relatív deformációval feszítik ki ε = 2, a minta ebből eredő hossza
L = 50 mm. Határozza meg az L0 minta kezdeti hosszát.
24. Mi legyen a stressz σ, amikor a dentint relatív deformációvá préseljük
ε = 2%. Olvassa el a dentin fogát egy rugalmas anyaggal, amelynek rugalmas modulusa E = 25 000 MPa?
25. Mi legyen az értéke a relatív alakváltozás ε nyomó fog dentin stressz alatt σ = 4400 MPa, feltételezve, hogy a dentin elasztikus anyagot egy Young rugalmassági modulusa E = 25,000 MPa?
26. Mekkora a fog dentin E elaszticitásának modulusa, ha a stressz σ = 250 MPa, a relatív törzs ε = 2%
27. Az ortopédiai fogorvosi elemek gyártásához használják
rozsdamentes acél huzal. Az L1 = 200 mm hosszúságú huzal merevsége k1 = 10 MN / m. határozzuk meg az L2 hosszúságú darab hosszúságának k2 merevségét 75 mm-rel a nagyobb keresztmetszet 1,5-szeresével.
28. Az ortopédiai fogorvosi elemek gyártásához használják
rozsdamentes acél huzal. Az L1 = 80mm hosszúságú huzalnak k1 = 5 MN / m merevsége van. Határozza meg az L2 = 85 mm huzalhosszúságú k2 merevségét 1,5-szer kisebb keresztmetszettel.
29. Az ortopéd fogászat hegesztett elemeinek gyártásához használjon rozsdamentes acélból készült huzalt. Egy darab L1 = 200 mm hosszú huzalnak k1 = 8 MN / m merevsége van. határozza meg az L2 = 50mm huzalhosszúság k2 merevségét ugyanaz a keresztmetszet.
30. Az ortopédiai fogorvosi elemek gyártásához használjon vezetéket rozsdamentes acélból. Egy darab L1 = 100 mm hosszúságú huzal merevsége k1 = 10 MN / m. Határozza meg az L2 = 300mm huzalhosszúság k2 merevségét azonos keresztmetszet.
31. Az ortopéd fogászat ólomelemeinek gyártásához használjon rozsdamentes acélból készült huzalt. Az L1 = 200 mm hosszúságú huzal merevsége k1 = 10 MN / m. határozzuk meg egy darab vezeték merevségét, 2-szer nagyobb keresztmetszettel és 1,5-szer hosszal.
32. Mekkora lesz a koboz merevsége? két párhuzamosan kapcsolt drótköteget az ötvözetből, amelyet a fogpótlások készítéséhez használtak? Mindkét vezeték egyforma hosszúságú, de különböző keresztmetszetű. Az első szegmens keresztmetszete kétszer akkora, mint a második. Az első szegmensek merevsége K1 = 5 MN / m.
33. Mi lesz a két, egymással összekapcsolt drótköteg merevsége, amelyet az ötvözetből készítenek a fogprotézisek összeszerelésére? Mindkét vezeték ugyanabból a keresztmetszetből áll, de különböző hosszúságú. Az első szegmens hossza kétszerese a másodiknak. Az első szegmens merevsége K1 = 10 MN / m.
34. Bizonyítsuk be, hogy a maximális Poisson arány μ = 0,5
35. Mutassuk meg, hogy az összenyomhatatlan anyagok esetében a Poisson aránya μ = 0,5
36. Hengeres minta, L0 = 15 mm kezdeti hosszúságú, aranyötvözetből
szakítószilárdsági vizsgálatokat végeztek. Ugyanakkor a hosszát L = 16,8 mm-re növelte,
és az átmérő d0 = 7 mm-ről d = 6,8 mm-re csökkent. Határozzuk meg az ötvözet Poisson μ arányát.
37. Az erő hatása alatt a minta deformációs sebessége hosszirányban λ = 2, keresztirányban pedig 0,625. Keresse meg a Poisson arányát ehhez az anyaghoz.
38. Keresse meg a λ minta deformációjának sokaságát hosszirányban, ha keresztirányban 0,77. A Poisson arány 0,3.
39. Keresse meg a λ mintának deformációinak számát keresztirányban, ha hosszanti irányban 1,8-es. A Poisson arány 0,32.
40. Mechanikai feszültség hatása σ = 150 MPa, elasztomer minta
háromszor megnyúlt. Mi az anyag nyíró modulusa G?
41. Keresse meg az elasztomer minta törzsének sokaságát egy szakítószilárdság hatására
mechanikai feszültség σ = 200 MPa, ha a nyíró modulus G = 40 MPa.
42. Határozzuk meg a nyírási modulust, ha a Young rugalmassági modulusa E = 300 GPa, és az együttható
43. Határozza meg az acél rugalmas E modulusát, ha a nyíró modulus G = 80 GPa, és
Poisson aránya μ = 0,33.
44. Az ábra vázlatosan hídprotézist mutat két bilaterális hordozóval
természetes A és B fogakkal. A koncentrált F erő 800 N-t alkalmaz a C pontban.
Határozza meg az A támasztófogat reakcióerőt, ha a = 3 cm és b = 2 cm
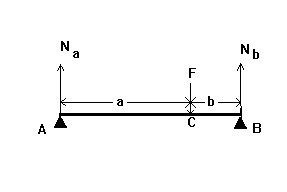
45. Az ábra vázlatosan hídprotézist mutat két kétoldalú alátámasztással
természetes A és B fogakkal. A 600 N koncentrált erőt alkalmazzuk a C pontban.
Határozza meg a B támasztófogat reakcióerőt, ha a = 4 cm, és b = 2 cm
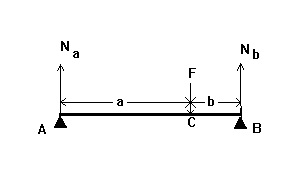
46. Az ábra vázlatosan hídprotézist mutat két bilaterális hordozóval
természetes fogak A és B. A koncentrált F erő egyenlő 900 N alkalmazható a C. pontban.
Határozzuk meg a keresztirányú Q erőt a x koordinátával = 3 cm-re, az A ponttól számítva,
ha a = 4 cm, és b = 2 cm
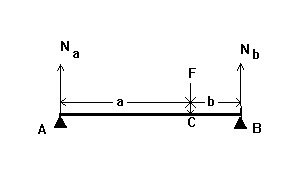
47.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 900 N alkalmazzuk a C pontban Határozzuk meg a keresztirányú erő Q keresztmetszetben a koordináta x = 5 cm, mérve az A pont, ha a = 4 cm, és b = 2 cm
48.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 630 N alkalmazzuk a C pontban Határozzuk meg a hajlítónyomaték M (x) a szakasz koordinátái x = 6 cm-re az A pont , ha a = 4 cm és b = 3 cm.
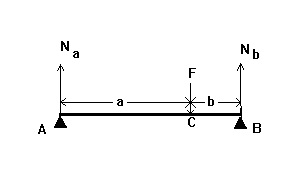
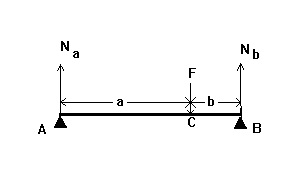
49.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 980 N alkalmazva a C pontban Határozzuk meg a hajlítónyomaték M (x) a szakasz a koordináta X = 3 cm-re az A pont , ha a = 4 cm és b = 3 cm.
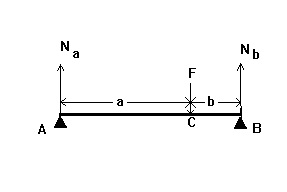
50.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő egyenlő 900 N alkalmazzuk a C pontban határozza meg a távolságot a referencia fogat egy, amelyben a hajlítónyomaték veszi a maximális értékét, ha a = 4 cm , és b = 3 cm.
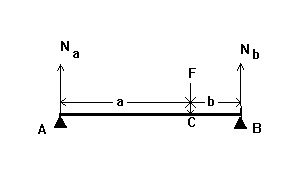
51.Na ábra vázlatosan két híd támogatja a kétoldalú természetes fogak és B. Koncentrált F erő, amely egyenlő a 980 N, alkalmazzuk a C pontban határozza meg a távolságot a referencia fogat egy, amelyben a hajlítónyomaték van beállítva, hogy M = 9H. m, ha, a = 3 cm és b = 4 cm.
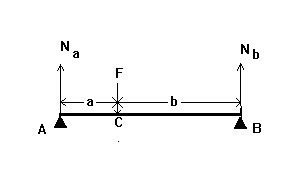
52. Az ábra a merev szilárdság és a folyékonyság hőmérsékleti határértékének függését mutatja a hőmérsékleten
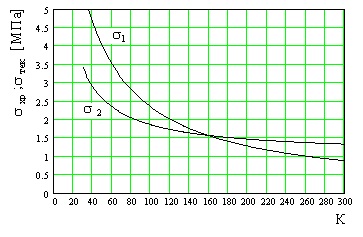
Milyen törésű vagy műanyag törést okoz a mintában 200 K hőmérsékleten?