Testimpulzus
4. blokk. Testimpulzus. Energy. A természetvédelmi törvények. Teljesítmény.
Testimpulzus (mozgásmennyiség). A lendület megőrzésének törvénye.
1. Minél hosszabb a cselekvési idő, annál nagyobb a test sebességének változása.
2. Az erő termékspecifikus hatását az I = F erőimpulzusnak nevezik # 916; t
3. A test impulzusa vektor fizikai mennyisége a test tömegének termékével megegyező sebességgel és a sebesség irányával. P = mv.
4. A test lendületének változása megegyezik az F # 916 erővel; t = mv -mv0. P = mv. F = # 916; p / # 916; t általánosabb megfogalmazása Newton második törvény.
5. Általában, a problémák megoldását tartják zárt rendszerben szervek - egy olyan rendszer, amely a kapott, a külső erők nulla. Figyelembe véve csak a belső erők, vagyis az erők belül a szervek között a rendszer: a rugalmas erő hatása, súrlódási erők a mozgás közben, a gravitációs erők, ha figyelembe vesszük a kölcsönhatás a szervek a világegyetemben, a Coulomb-erő az elektromos kölcsönhatást, mágneses erő, stb ...
6. A lendület megőrzésének törvénye. A zárt szervrendszer teljes lendülete állandó marad a rendszer testének bármely kölcsönhatásához. A zárt rendszer testének pillanatnyi vektorösszege az interakció előtt egyenlő a rendszer testének pillanatnyi vektorösszegeivel az interakció után. Az előrejelzésekben: m1v01x + m2v02x = m1v1x + m2v2x
7. A vízi hajtás olyan mozgás, amely akkor következik be, ha bizonyos részből egy bizonyos testből leválik valamilyen sebességgel. Lövés, rakéta, polip, felfújható labda stb.
8. Mi határozza meg az erő hatását? (Idő, koordináta). Az erő jellemzője az erő impulzus. Az erő térbeli jellemzője a munka.
Munkát. Energy. A megőrzés és az energiaváltozás törvényei. Teljesítmény.
9. Munka - fizikai mennyiség, amely megegyezik az erő előrejelzésének termékével
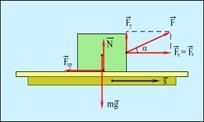
10. Hogyan függ a munka az elmozdulás és az erő közötti szögtől?
· # 945; = 90 °, a merőleges erők munkája egyenlő 0 = A = FS = 0.
· # 945; = 180o, az ellenállási erők negatívak A = -FS.
11. Mi a helyzet a támogatás, a súrlódás, a gravitáció reakcióerőivel?
· A gravitációs munka A = mgh1-mgh2 független a pályaszakasz formájától, és nulla a zárt kontúr mentén.
· A kapott erő hatása A = mv22 / 2-mv12 / 2
12. A potenciális erők olyan erők, amelyeknek munkája csak egy térbeli pont kezdeti és végső helyzetétől függ. A gravitáció és a rugalmasság ereje potenciális erők.
20. Egy fizikai mennyiség, amely jellemzi a test képességét a munkára, az energia [E] -J.
21. A test potenciális energiája az interakció energiája. A Föld felett emelt testek elasztikusan deformált testek. Ep = mgh, Ep = kx2 / 2.
22. A gravitációs munka pozitív lesz ősszel. A potenciális energia csökken. Az emelés gravitációs hatása negatív lesz. A potenciális energia emelkedik az emelkedéssel.
22. Minden zárt rendszer hajlamos arra, hogy a legalacsonyabb potenciális energiával rendelkező állapotba kerüljön.
23. A Föld felszínén a gravitációs erő potenciális energiája minimális és egyenlő az Er = -GMm / R3 értékével. A Földről eltávolítva 0-ra emelkedik, majd nem változik.
24. A test kinetikus energiája a mozgás energiája Ek = mv22 / 2
25. A test kinetikus energiájának elmélete: A kinetikus energia változása megegyezik a keletkező erő munkájával. A = # 916; Ek
26. A rendszer teljes mechanikai energiája egyenlő a kinetikus és potenciális energiáinak összegével.
27. A mechanikai energia változásának törvénye. A rendszer mechanikai energiájának változása megegyezik az összes nem potenciális erő (pl. Súrlódási erők) munkájával.
28. A mechanikai energia megőrzésének törvénye: Ha zárt rendszerben csak a potenciális erők járnak el, akkor a rendszer teljes mechanikai energiája a rendszer testének bármilyen kölcsönhatásaiban marad.
31. A munkát végző mechanizmusokat egy hatékonysági tényező jellemzi. A hatékonyság megegyezik a hasznos munka és az elkötelezettség viszonyával. # 951; = An / Ac, és százalékban mérve.
32. Teljesen rugalmas ütközés olyan ütés, amelynél a testek deformációja kiderül, hogy megfordítható. A mechanikai energia megőrzésének törvényét és a lendület megőrzésének jogát is teljesítik. Rugalmas ütközés eredményeképpen az azonos testek sebességváltást végeznek. Központi ütközés esetén a mozgó golyó leáll, míg az álló golyó megszerzi a mozgó golyó sebességét (abban az esetben, ha a gömbök tömege megegyezik).
33. Az abszolút rugalmatlan hatás egy olyan ütés, amelyben a testek az interakció eredményeképpen mozognak. Csak a lendület megőrzésének törvénye teljesül.
34. A hidrodinamika törvénye:
35. Az áramló folyadék nyomása különböző átmérőjű csövekben nagyobb annál nagyobb, mint a cső keresztmetszete. Ez az energia megőrzésének törvényéből és a csővezetékben lévő vízsugár folytonosságának tulajdonságaiból következik. Mivel ugyanazon mennyiségű víz áramlik át a cső keresztmetszetén keresztül egységnyi idő alatt, az áramlás sebessége a kis átmérőjű csövekben növekszik. Összesen mechanikai energia a víz áll a kinetikus energia a mozgás és a potenciális energia a kölcsönhatás a falak a cső és állandó marad bármely részét a cső. Amint a kinetikus energia nő, a potenciális energia, és így a nyomás csökken.
CÉLKITŰZÉS 1. A 80 kg súlyú rakomány közvetlenül az ejtőernyő kilövése után
gyorsabban mozog, majd elérte a 10 m / s sebességet 500 m tengerszint feletti magasságban
mielőtt a leszállás egyenletesen mozog.
Keresse meg: A. Teljes mechanikai energiát 500 m magasságban.
B. Teljes mechanikai energia a leszállás és az idő alatt
mozgás 500 m magasságból.
C. Mi a légellenállási erők munkája az egységes mozgás során?
B.E2 = Ek + Ep = mv2 / 2 + 0, S = Vt
C. A nem potenciális erők hatnak a testre - az ellenállás erői.
Ezeknek az erőknek a munkája megegyezik az A = teljes mechanikai energia változásával # 916; E = mgH
CÉLKITŰZÉS 2. A 10 g-os golyó 600 m / s sebességgel repül, egy kötélen felfüggesztésre kerül
Egy 10 kg-os súlyú fából készült rúd beakad.
Találd meg: A. Bullet impulzus és a golyó kinetikus energiája.
B. Keresse meg a rúd által kapott sebességet.
C. Mekkora magasságban emelkedik a rúd, miután eltalál egy golyót.
ZADACHA3. Egy 60 méteres súlyú úszó, öt méteres toronyból ugrálva a vízbe 2 méteres mélységbe esett.
Keresse meg: A. Az úszó összes mechanikai energiája 5 m és 3 m magasságban a vízszint felett.
B. Swimmer sebesség vízbe merítés előtt.
C. A vízben lévő ellenállás erői és a vízben való mozgás ideje.
SolutionA.E1 = Ek + Ep = 0 + mgH - a vízszinthez viszonyítva. Vezetés közben
a levegőben az ellenállók elhanyagolhatók. Aztán a teljes mechanikai energiát
E2 = E1. És 5 m tengerszint feletti magasságban, 3 m magasságban, és teljes merítés előtt
a mechanikai energia ugyanaz.
B. A mechanikai energia megőrzésének törvényéből a vízszinthez viszonyítva van
E2 = Ek + Ep = mv2 / 2 + 0 - a vízszintbe lépés előtt a vízszintes nulla értéknél nulla =
C. A nem potenciális erők hatnak a testre - az ellenállás erői. Ezeknek az erőknek a munkája megegyezik az A = # 916 teljes mechanikai energia változásával; E. A = mgH, mert 2 m mélységben a mechanikai energia nulla.
PROBLÉMA 4. Egy műanyag golyó tömege m, amely egy szálon lóg, eltér az egyensúlyi pozíciótól
H magasság és engedje el. Találkozik egy másik 2 m tömegű golyóval, egyenlő hosszúságú szálakkal.
Keresse meg: A. A labda teljes mechanikai energiája az ütközés előtt és lendülete.
B. A golyók sebessége abszolút rugalmatlan ütközés után.
C. Milyen magasságban fognak fel a golyók az ütközés után?
Megtaláljuk a sebességet a mgh = mv2 / 2 energiamegtartás törvényéből
2.P = mv a test lendülete (a mozgás nagysága).
5. A = FxSx A = FScos # 945; - erőszak
· # 945; = 90 °, a merőleges erők munkája egyenlő 0 = A = FS = 0.
· # 945; = 180o, az ellenállási erők negatívak A = -FS.
10.Ep = Mgh a test potenciális energiája felemelt a Föld felett
11.Ep = kx2 / 2 - egy elasztikusan deformált rugó potenciálja
14. A = # 916; Ek - az eredményes erő munkája
15.E = Ek + Ep a teljes energia
16.Ek1 + Ер1 = Ек2 + Ер2 - a mechanikai energia megőrzésének törvénye
17. # 916; Emex = A külsõ erõk - az energiaváltozás törvénye
19.P = Fv - pillanatnyi teljesítmény
20. - a hatékonysági hatékonysági tényező