Számítógépes grafika tanfolyam - 4. feladat
A feladat célja a geometriai objektumok két- és háromdimenziós térben való működtetésének képessége, a morfálás geometriai objektumainak koncepciója, az egyszerű vizuális megjelenítés készsége az OpenGL segítségével.
Olyan programot kell létrehoznod, amely lehetővé teszi, hogy egy bizonyos alakú két- és háromdimenziós objektumokat alakítson ki.
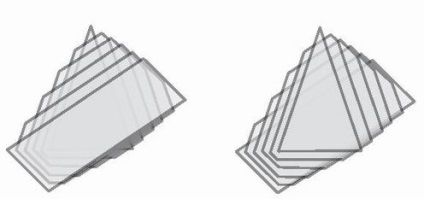

1. ábra Példák a két- és háromdimenziós terek morfizálására.
Lehet letölteni egy példát a feladat végrehajtására a háromdimenziós térben.
A javasolt algoritmus
A sík domború figurák lehetséges megvalósítását adjuk. Az algoritmus nyilvánvalóan a háromdimenziós ábrák esetében általánosítható.
Az algoritmus részletes leírása megtalálható a csatolt cikkben.
Tekintsük azt a folyamatot, amely egy konvex A ábrát egy konvex B ábrán mutat.
Hagyja a morfizálást a [0,1] időintervallum alatt. Meg kell adni az AB (t) értéket minden egyes t időpontnál [0,1], úgy, hogy AB (0) = AB AB (1) = B. AB idővel változik.
I. fázis. Ábrák bemutatása.
Az A ábra arcain keresztül vonalak húzódnak - nevezzük őket határvonalaknak. Az egyenes vonal által határolt szám A ''.
A határvonalak párhuzamos fordítását olyan módon végezzük, hogy A "a B ábrát tartalmazó minimális szám (2. Az arcok párhuzamos átadását a 2a, 2b, 2c ábrák mutatják. Az 1. ábrán. A 2d az eredményt mutatja: az eredeti "leírt" az utolsó. Ha az átruházást véges időre elvégezzük, az A-nak A-ba történő átalakítását kapjuk ":
Ugyanígy létrejön az A kép B ábrája és a B '= B' (t) morfálás. A kép felépítését az 1. ábrán mutatjuk be. 3a-d.
2. ábra Számadatok leírása.
Fig.3 ábra leírása.
II. Morfium.
A konstrukció egy folytonos morfium számok az A és B egymással egyidejűleg képződött morfium A az A „és B” a B minden t a [0,1] AB „(t) van kialakítva ábra. amely az A '(t) és a B' (t) metszéspontja. A közbenső ábrák előállításának folyamata a 3. ábrán látható. 4a. Az eredmény a Pic. 4b.
Ábra: A morfizálási folyamat.

Ábra: A morfálás folyamata.
AB '(0) = A
AB '(1) = B
Az AB idővel simán változik
A háromdimenziós eset algoritmusának részletes leírása
Megjegyzés: azoknak, akik az elmét lineáris algebra segítségével szeretnék gyakorolni, javasoljuk, hogy hagyja el ezt a szakaszt. A többit részletesen leírjuk, hogyan oldjuk meg a problémát.
1. lépés: Az ábrák ábrázolása.
Tegyük fel, hogy a merőlegesek A ábra kifelé irányulnak, fogják hívni egy fél-térben a relatív szembe (vagy egy sík tartalmazó kötött) számadatok és a pozitív (P + (a)), ha a normál az arc irányul, hogy a fél-térben.
Állítsa be a morfálás felbontását (az A és B közötti köztes számok számát) - N.
Az A arcát vesszük. Az azt tartalmazó síkot jelöljük, a. A minimális vektort kiszámítjuk. oly módon, hogy az A és B ábrák teljesen az a. d-ből való átváltással nyerhető.
A B. ábra összes csúcsa között megtaláljuk a legtávolabbi M csúcsot a síkból a és a P + (a) -on. A vektor egy tetszőleges a-tól M-ig terjedő vektorra való vetülete a normál a értékre a szükséges d vektor.
Jelöljük az a-ból kapott síkot, d + (i / N) hozzáadásával. mint (i).
Az A lépések mindegyik oldalára megismételjük az 1. lépést. Az egyes i-hez tartozó kapott felületeket A (i) jelöli.
A B ábrán ugyanazt az eljárást ismételjük meg, azzal a kivétellel, hogy a B ábrán látható b (i) jelölések jelentése b + d * (N-i / N).
2. lépés Morfizálást generál.
A morfálás i-edik lépésének megszerzéséhez meg kell találni egy olyan számot, amelyet az A (i) és a B (i) síkok halmazai határolnak. E csoportok egyesülését C (i) -nek nevezzük.
Megtaláljuk a pontok Q 'pontját, ahol a C (i) három vagy több arc metszi.
A Q-tól a Q-tól kapjuk meg, ha a C (i) -ben lévő legalább egy sík pozitív féltérben lévő pontjait eldobjuk.
Formázza az intermedier ábráit a Q pontokból.
Minden C (i) síkon megtaláljuk a Q pontokat. A hozzá tartozó pontok (a síktól a pontig terjedő távolság nulla). Ezek a pontok az arc csúcspontjai.
Számoljuk a pontokat úgy, hogy konvex sokszöget alkotnak. Válasszuk ki a b vektort. összekapcsolva két, tetszőlegesen kiválasztott A és B pontot a kérdéses készletből. Jelöljük n a normál értéket a síkra, amelyhez a készlet pontjai tartoznak (a sík a készlet bármelyik három pontjából megtalálható). A készlet pontjának számozását a szög szögének megfelelően kell elvégezni, amelynél a b körül az A körül forgatni kell, hogy az n és q áthaladó sík. a készletbıl eltérı A és B pontot tartalmazott, azaz a vektorok b és c = AC között. Megjegyzés: a számozás során ne feledje el, hogy meg kell találnia a kapott arc normálját.
Megjegyzés: a 3. lépésben megoldott feladat egy konvex hajótest keresése a Q pontok készletéhez. Több elegáns algoritmus létezik a probléma megoldására. Az ilyen algoritmusok végrehajtása egy alkalom arra, hogy bónuszt kapjunk.
Kötelező rész
A kötelező rész feltételezi a domború sokszögek morfizálását kétdimenziós térben. A programban mereven meghatározott kezdeti és végső sokszögek találhatók. A felhasználó parancsára a morfizálási folyamat elindul.
A morfálás folyamatának jól láthatónak kell lennie a képernyőn - a folyamat sebességének ésszerűnek kell lennie.
Az első és a végső számoknak jelentősen különbözniük kell: csúcspontok, élek stb.
A síkszámok helyett (vagy azok mellett) a háromdimenziós térben lehet morfizálást végrehajtani - ez a lehetőség több pontot ad. A folyamat látható az OpenGL könyvtár használatával.
További rész
Az alábbiakban felsoroljuk azokat a lehetőségeket, amelyekhez további pontokat kaphat.
A morfálás előrehaladásának vezérlése: a gombok előre, hátra, szüneteltetése, a morfálás egy lépése.
Poligon vagy sokszög modellek olvasása fájlból.
A kétdimenziós eset fájlformátuma:
Mindegyik sor tartalmazza a térközzel elválasztott csúcs koordinátákat. A csúcs száma megegyezik a vonalszámmal. A csúcs számozása az óramutató járásával megegyező. A csúcs koordinátái valós számok, a tartomány [-1,1].
A háromdimenziós eset fájlformátuma:
MESH_FILE. =
MESH_VERTEX_LIST <>
MESH_FACE_LIST <>
>
Megjegyzés: a leírásban a szimbólum <и лексемы MESH_VERTEX_LIST, MESH_FACE_LIST нужно рассматривать как строковые константы. - целое неотрицательное число, - вещественное число в диапазоне [-1,1].
Színek vagy textúrák összekeverése. Színezés - a fokozatos színváltozás az egyik alak átalakításának folyamatában. A textúra összekeverése: a textúrák az eredeti és a target polyhedron modellekre kerülnek. A közbülső morfamodellek szerkezete a forrás és a végleges modellek textúráinak keveréke, amelyet többnyelvű OpenGL segítségével nyernek (lásd a feladatok anyagait).
Példák a poligonok és a poliéderek modelljeire:
bejegyzés
A formatervezés nem különbözik a megszokottól.
ZIP-fájlt a forráskód és a futtatható fájlokat, nevezett eljárás szerinti GZV_nnnnnnnn.zip (ahol G - az utolsó számjegy a csoport szám, Z - feladat száma, V - amelyben a verziószámot, nnnnnnnn - diákigazolvány szám), hogy küldjön [email protected]. msu.su
Például egy diák 206 csoportok tanulói azonosító száma 06529042, mely frissített (második) változata a második feladat a program küldjön egy fájl nevét 622_06529042.zip.
Ne felejtsük el elhelyezni a readme.txt fájlt az archívumba. A fájlban írja le a program interfészt (az algoritmust a programhoz, a menüpontokhoz, a vezérlőgombokhoz)
A munka eredményei
Az eredmények az interneten és / vagy a 703-as terem közelében állnak.
jegyzetek
- A feladat szigorúan egyedi. Együttmûködésre vagy kódkódok cseréjére -5 pontot rendelünk minden résztvevõhöz, ha a csapatmunka tényét a feladatok readme.txt-jában nem határozta meg.
- Javasoljuk, hogy írjon egy programot a Windows család számára. Más operációs rendszerekre való írás nem kívánatos, és késlelteti az ilyen munkák ellenőrzését.