Működési képlet a lencse görbületi sugarának meghatározásához
Vékony filmben egyenlő vastagságú interferencia sávok, azaz sötét vagy világos sávok megfelelő állandó érték a film vastagságának (d), megfigyelhető közötti légrés az érintkeztetés egymással egy lapos lemez felülete és a konvex gömbölyű felülete a lencse (lásd. 5. ábra).
Ebben az esetben a légréteg vastagsága fokozatosan növekszik a lencse középpontjától az éleiig. A normál (merőleges a felszínre) fény előfordulása esetén az egyenlő vastagságú sávok koncentrikus körök formájában vannak, amelyeket Newton gyűrűinek neveznek.
Ha egy monokromatikus fénysugár esik az objektívre, akkor a légréteg felső és alsó határait tükröző fénysávok egymásba ütköznek.
Mivel, ellentétben a fent megadott példában, a fény hullám reflexió történik azon a ponton B a levegő-közepes üveg, és nem az üveg-levegő a 4. ábrán látható, a λ / 2-t adunk, hogy az summand L1 és a (19) képletű a kezdeti részében úgy fog kinézni:
Ez azt jelenti, hogy az optikai útkülönbség ebben az esetben kétszerese a légrés (2d) vastagságának (a levegő refrakciós indexe = 1).
Végül:
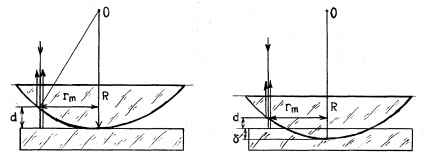
5. ábra. Az esemény előfordulási sémája Fig.6. Deformációs számvitel
Newton gyűrűje
Sötét gyűrű alakul ki, ahol az optikai ösvénykülönbség egyenlő a félhullámok páratlan számával (lásd 16):
azaz egy holtjáték vastagságában
ahol m = 0,1,2,3. gyűrűszám.
Az m-es sötét gyűrű (rm) sugara az AOC háromszögből (lásd az 5. ábrát)
ahol R a lencse görbületi sugara. Feltételezve, hogy a légrés értéke azon a helyen, ahol a gyűrűk származnak, kicsi (azaz d "R), akkor írhatunk:
Ebből a képletből látható, hogy a lencse görbületi sugara a Newton-gyűrű sugara és a légrés mennyisége a gyűrű származási helyén mérhető. A Newton-gyűrűk sugara mérhető skálával mérhető mikroszkóppal mérhető. Annak érdekében, hogy ne mérjük a rés méretét (egyébként nem világos, hogyan kell kísérletesen végrehajtani), a sötét gyűrűk (24) megjelenésének interferencia feltételeit használhatjuk.
Ezután a lencse görbületi sugara a Newton-gyűrű sugarának, a használt fény hullámhosszának és a mérendő gyűrűszámnak megfelelően kifejezhető:
A (28) képlet segítségével a görbület sugara meghatározásához hiba léphet fel, mert egy pont a kontaktlencsék és a lencse üveglap deformáció lehetséges nagysága összemérhető a fény hullámhossza, így a használata terminálok alapján 5. ábrán (lásd. a képlet 26,27,28) helytelen lesz.
A légrés kísérletileg megfigyelt értéke kisebb lehet, mint az 5. ábrából kapott elméleti érték az üveglap és a lencsék deformációjával (δ) (lásd a 6. ábrát). Ezért, egy tényleges kísérlet (27) képletű helyett a vastagsága a légrés (d) a szükséges összeget, hogy helyettesítse a vastagsága a légrés, és a mérete a lencse és üveglap deformáció (d + δ) .Given, hogy a feltétel bekövetkezése sötét gyűrűvel (24) határozza csak a vastagsága a rés, a következő képletet kapjuk, amely összeköti a Newton-gyűrűk sugarait a lencse görbületi sugaraival:
Kívánatosabb, hogy a Newton-gyűrű sugara (Dm) átmérőjével kísérletileg helyettesítse, ebben az esetben a (29) képlet a következő alakú:
Tól (30) látható, hogy a tér a átmérője Newton gyűrűk (dm2) arányos a sorszáma a gyűrű (m) .Ha ábrázoltuk dm2 = f (m), a kísérleti pontok fekszenek egy egyenes vonal, és a meredeksége ennek egyenes vonal (α ) 4Rλ, tehát a lencse görbületi sugarának megtalálásához szükség van a Dm2 = f (m) függvény grafikonja segítségével
majd a lencse görbületi sugarát a következő képlet segítségével számoljuk:
A deformáció következtében a lencse középpontjában egy kör alakú sötét folt található, amely megfelel a légrés nulladik vastagságának. A központi sötét folt átmérőjének (Newton gyűrűje, amelynek számszáma m = 0) a lencse alakváltozásának értékét a következő képlet határozza meg: