Gyűrűs szektor terület - képlet, számítási példa
A körkörös gyűrű egyik szektora egy lapos alak, amely a két kört ív közötti sík egy részét képezi, amelynek egy közös középpontja van, és különböző radii által határolt két sugárirányú vonal, amelyeket egy nagy sugarú ív végeire vonnak le.
A gyűrű ágazatának alakja, a külső és a belső sugáron keresztül
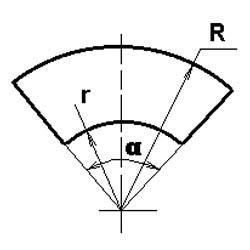
Adjuk meg az R sugár körét és egy r sugara körét. És R> r. Ezeknek a köröknek a központjai kompatibilisek. Két önkényes pontot veszünk egy nagy körű körön. Húzza azokat az a szöget alkotó sugarakra. Ezek a sugarak levágtak néhány ívet a körökből. A körívek köré és a körívek vége felé húzódó ábrák közé soroljuk a gyűrű szektorát, amelyben R a külső sugár, r a belső sugara.
Ekkor a szám mezője megegyezik a nagy sugárral rendelkező kör szektorának és a kisebb sugarú kör szektorának területe közötti különbségnek.
Az r sugarú kör szektorát a következő képlet adja meg:
ahol l az ív hossza egyenlő
Az ív hossza kifejezését a szektor területének képletére helyettesítjük. Kapunk:
Az R sugárral rendelkező kör területét a következő képlet adja meg:
ahol L az ív hossza egyenlő
Az ív hossza kifejezését a szektor területének képletére helyettesítjük. Kapunk:
Ezután a gyűrű területe:
Így a gyűrű ágazatának területe megegyezik a gyűrű egységszektorának területének termékével, vagyis az ágazatnak megfelelő központi szög mértékével az egységgel megegyező mértékű központi szögnek megfelelő szektornak.
A képlet a következőképpen alakul:
Példa egy gyűrűszektor területének kiszámítására, ha sugara ismert.
Keresse meg a gyűrű szektorának 30 ° -os szögét. ha külső sugara 14, a belső sugara 8.
A gyűrű területét a következő képlet adja meg:
Az értékek a probléma állapotából történő helyettesítésével rendelkezünk: