A háromszög szögének összege

LÉSZONI ELMÉLET: A háromszög szögeinek összege.

• A diákok tudásának megerősítése és tesztelése a témában: "A háromszög szögének összege";
• Háromszög szögének igazolása;
• A tulajdonság alkalmazása a legegyszerűbb problémák megoldásában;
• Történelmi anyag felhasználása a diákok kognitív tevékenységének fejlesztésére;
• Pontossági edzés a rajzrajzokban.

• Ellenőrizze a tanulók képességeit a problémák megoldására.

1. háromszög;
2. A háromszög szögének összegére vonatkozó tétel;
   
3. Példa a feladatokra.

Fájl: O.gif Triangle egyenes vonalú, része a sík által határolt három vonalszakaszok (oldalán a háromszög (a geometria)), amelynek páronként egy közös végén (háromszög csúcsa (geometria)). Egy háromszög, amelynek hossza minden oldal egyenlő, egyenlő oldalúnak. vagy helyes. Egy háromszög két egyenlő oldallal egypólusú. A háromszöget akut szögűnek nevezik. ha minden szöge éles; négyszögletes - ha egyik szöge egyenes; feltűnő - ha egyik sarka tompa. Háromszög (geometriában) nem lehet, hiszen mindhárom szög összege két derékszög (180 °, vagy radian, p) egyenlő. A háromszög területe (geometriában) ah / 2, ahol a a háromszög egyik oldala, amelyet a bázisához vett, h pedig a megfelelő magasság. A háromszög oldalai a feltételtől függnek: mindegyikük hossza kisebb, mint az összeg, és nagyobb, mint a másik két oldal hosszának különbsége.

Fájl: O.gif A háromszög a legegyszerűbb poligon, 3 csúcs (szög) és 3 oldal; a három ponttal határolt sík egy része és három szegmens, amelyek párhuzamosan kapcsolják össze ezeket a pontokat.
Három olyan hely, amelyek nem fekszenek egy soron, egy és egy síknak felel meg.
Bármely poligon háromszögekre osztható - ezt a folyamatot triangulációnak nevezik.
Van egy matematikai szakasza, amely teljes egészében a háromszögek szabályszerűségének tanulmányozására irányul - Trigonometria.

A háromszög szögének összegére vonatkozó tétel.

Fájl: T.gif A háromszög szögeinek összege egy euklideszi geometria klasszikus tétele, azt állítja, hogy a háromszög szögeinek összege 180 °.

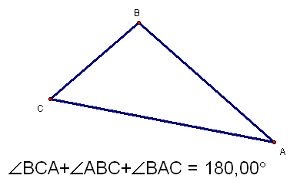
Adjuk meg az ABC-t. Egyenes vonalat húzzon párhuzamosan (AC) a B csúcson és jelölje meg a D pontot úgy, hogy az A és D pontok a BC vonal két oldalán feküdjenek. Ezután a szög (DBC) és a szög (ACB) megegyeznek azokkal, amelyek keresztirányban fekszenek a BD és AC párhuzamos vonalakkal és a szekantummal (BC). Ezután a háromszög szögeinek összege a B és C csúcsaiban megegyezik a szög (ABD) értékével. Az ABC háromszög csúcsa A szög (ABD) és a szög (BAC) pedig BD és AC és szekundum (AB) párhuzamos vonalakkal egyoldalú, összegük 180 °. Következésképpen a háromszög szögének összege 180 °. A tétel bizonyított.

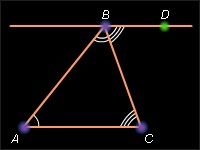
A háromszög külső sarkának megegyezik a háromszög két szögének összegével, nem pedig szomszédosán.

Adjuk meg az ABC-t. A D pont az AC vonalon helyezkedik el, hogy A a C és D közé esik. Ezután a BAD az A és A + BAD = 180 ° -os háromszög sarkánál helyezkedik el. De A + B + C = 180 °, ezért B + C = 180 ° - A. Ezért BAD = B + C. A következmény bizonyult.

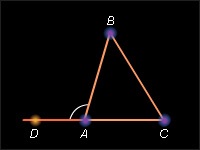
A háromszög külső sarkánál nagyobb a szomszédos háromszög bármely szöge.

A háromszög külső sarkának egy szöge van a háromszög egyes szögének közelében. Bizonyítsuk be, hogy a háromszög külső sarkája megegyezik a háromszög három szögének összegével, amelyek nem szomszédosak.

(1. ábra)

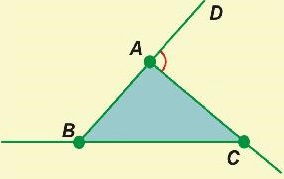
Hagyja ABC ∠DAC - külső (1. Ezután ∠DAC = 180 ° -∠VAC (szomszédos szögek tulajdonságai alapján), a ∠B + ∠C = 180 ° -∠VAC háromszög szögének összegével. Ebből az egyenlõségbõl kaptunk ΔDAC = ∠B + ∠C

A hiperbolikus geometria összege háromszög szögeinek mindig kisebb, mint 180. euklideszi geometriában ez mindig megegyezik a 180. geometria, a Riemann összege háromszög szögeinek mindig nagyobb, mint 180.

A matematika történetéből:

Euklid (III. Köztársaság) a "kezdet" munkájában a következő definíciót adja: "A párhuzamos vonalak olyan egyenesek, amelyek ugyanabban a síkban vannak, és mindkét irányban korlátlanul folytatódnak, nem találkoznak egymással sem" .
Posidonius (I-ben BC) "Két egyenes vonal ugyanabban a síkban, egyenlő távolságra egymástól"
Az ókori görög tudós, Papp (III. Kr.e.) bevezette a párhuzamos vonalak - a = jelet. Ezt követően az angol közgazdász Ricardo (1720-1823) ezt a szimbólumot egyenlő jelként használta.
Csak a XVIII. Században kezdte használni az egyenes vonalak párhuzamosságának szimbólumát - a szimbólum ||.
Egy pillanatra nem szakad meg a generációk közötti élő kapcsolat, minden nap megtanuljuk az őseink által felhalmozott tapasztalatokat. A görögök a megfigyelések alapján, és a gyakorlati tapasztalatok következtetéseket levonni feltevése, akkor a tudósok a találkozókon - szimpóziumok (szó szerint „lakoma”) - ezek hipotézisek próbálta igazolni és bizonyítani. Abban az időben volt egy kijelentés: "Egy vitában az igazság születik."

1. Mi a háromszög?
2. Mit mond a háromszög szögének összege?
3. Mi a háromszög külső sarkában?

Az alkalmazott források listája:

A lecke felett:

Felteheti a kérdést a modern oktatásról, kifejezhet egy ötletet, vagy sürgős problémát megoldhat az Oktatási Fórumon. ahol nemzetközi szinten új gondolat és akció oktatási tanácsa gyűlik össze. Blog létrehozásával nem csak a kompetens tanár állapotát javíthatod, hanem jelentősen hozzájárulhatsz a jövő iskolájának fejlesztéséhez. Az Oktatási vezetők céh nyitja meg kapuit a legmagasabb rangú szakemberek számára, és felkéri Önt, hogy működjenek együtt a világ legjobb iskoláinak létrehozásában.