Bibliográfiai leírás:
1. Bevezetés A modern irányítási elmélet egyik legfontosabb problémája az a rendszer, amely a kívánt minőséget biztosítja, amikor egy külső zavar befolyásolja az objektumot. Az erőteljes kontroll problémáinak osztályában nagyszámú módszer és megközelítés létezik a probléma megoldására. A legerőteljesebb elmélet és bibliográfia ezen az oldalon található [1]. A harmonikus oszcilláció belső modelljét használva létrejött vezérlő algoritmust [2-5] -ben kaptuk. Azonban az ellenőrzési rendszerek szintézisének egyik legfontosabb problémája, amelyek lehetővé teszik a zavarok kompenzálását, feladata egy olyan jel előállítása, amely információt hordoz róluk, és lehetővé teszi annak felhasználását a szükséges becslések eléréséhez. Ezt a problémát oldották meg [6-9], mely a kiegészítő áramkör módszer, amely lehetővé teszi, hogy válasszon ki egy jelet hordozó interferencia információ megszerzése a szükséges becsléseket és kompenzálja a nemkívánatos zaj hatásainak a beállítható paraméterek. Ez a tanulmány egy módszer építésére ellenőrző rendszer lineáris objektum, hogy az összes paraméter ismert, és a bemeneti és kimeneti ellenőrzött zavarok és zavar ezeknek a különböző, és nem igényel semmilyen a priori ismeretek paramétereinek külső zavarások. A tervezett vezérlőrendszer lehetővé teszi az interferencia hatását az ellenőrzött változóknak egy adott pontossággal történő kompenzálására, és függetlenül azoktól, amelyek a rendszer bemeneténél nem mérhető, korlátlan zavart okoznak. A fő eredmények a rendszerek konstruktív beágyazásának technológiája [10] és a kiegészítő kontúr módszer [6-9] segítségével történtek.
A vezérlő objektum az (1) - (3) egyenletek formájában van megadva:
(3) ahol. . . - az állami, a vezérlő, a mért és az ellenőrzött paraméterek vektorai, - a külső zavarok vektora, - a rendszermodell statikus összeköttetéséből származó zaj; - kezdeti feltételek; - a megfelelő megrendelések számszerű mátrixai. Szükséges egy algoritmust szerezni a vezérlési rendszer működésére, amely biztosítja a célállapot (4) teljesítését a következő helyen:. ahol - elég kicsi érték, - az az idő, amely után a rendszer működésbe lépése után a szükséges dinamikus pontosságot biztosítani kell.
A pár irányítható, és a pár megfigyelhető;
a rendszer bemeneténél a perturbáció határolt függvény;
ii) a rendszer kimenetén belüli interferencia korlátozott funkció;
v) az (1) - (3) összes mátrix ismert.
A nyilatkozat feltételei között egyéb korlátozások is megjelennek.
A kontrollvektorot formában alakítjuk ki
(5). hol van a kiegészítő mérésszabályozó? A szabályozó numerikus mátrixa.
Előzetes információk a mátrixok kanonizációjáról
Ha a mátrix nem teljes (irreverzibilis), tartalmaz lineárisan függ a sorok és / vagy oszlopok. Leírni a lineáris függés és függetlenség a sorok és oszlopok a mátrix kényelmesen használható fogalmát zérusosztó maximális rangot és kanonizatorov. [10] kanonizálásról azt elemzi nem feltétlenül egyedi bomlás bármilyen mátrix mérete és fokozat négy mátrixok kielégíti a következő egyenletet a blokk írási és ahol - a bal és jobb zérusosztó maximális rangot, és - bal és jobb kanonizatory (-. Azonosságát méretű mátrix). Bármely mátrix bal (jobb) elválasztó maximális rangot nulla összes jellemző lineáris kombinációi a függő sorok (oszlopok) az eredeti mátrix szerint a személyazonosságát (). Megoldásában a mátrix egyenletek által használt szentté fogalmának konszolidált kanonizatora. számított képlet szerint, és kielégítő a rendszeresség feltételeknek Neumann. . Konszolidált kanonizator ismertet egy sor lineárisan független kombinációi sorok és oszlopok az eredeti mátrixban. A konkrét esetben, ha a konszolidált kanonizatora pszeudoinverze Moore - Penrose. Egy mátrix teljes rangú tartógerenda konszolidált kanonizator egybeesik a megfelelő elválasztó egység. mátrix teljes rangú oszlop - a baloldali osztó egység. Jobb (bal) elválasztó egység mátrix mérete teljes öltés (az oszlop) mátrix rang () kielégíti a feltételt (). Annak meghatározására, a paramétereket a vezérlő, a nyilatkozatot megfogalmazott VN Bükk [10, s.473]. Elfogadása 1. Rendszer (1) - (3) az adott mátrixok van invariancia perturbációkra abban az értelemben, tozhdestvatogda és csak akkor, ha a következő feltételek: 1) létezik egy nem nulla mátrix nyomtávú invariancia. amely kielégíti azt az állapotot 2) mátrix hatékonyságát zavarások a beállított, ahol - a tetszőleges numerikus mátrix megfelelő méretű, és 3) a rendszer által lezárt bármely vezérlő (6) a készlet (6), ahol - a mátrixok megfelelő méretű tetszőleges elemek [10].
-
A menedzsment szintézise
A szabályozó törvényt (5) alkalmazzuk, majd az (1) - (3) objektum egyenlete a formát veszi fel. ahol a Hurwitz-mátrix, vagyis a sajátértékek kielégítik az állapotot. A szerkezeti rögzítési rendszer technológiai meghatározásával képletű szabályozó (6), keresünk annak érdekében, hogy az átviteli függvény a zavart a szabályozott kimeneti nullává válik, és ennek megfelelően, az alkatrész el van tolva. Ezután a rendszer reprezentációját bemeneti kimenet formájában (7) fordítjuk, ahol a differenciálási operátor; . - a mátrix algebrai kiegészítéseinek átültetett mátrixa; . . Ezután használjuk a segédáramköri módszert, és kiválaszthatjuk az interferenciával kapcsolatos jeleket hordozó információkat, amelyekhez a (8) egyenletben leírt alrendszert alkalmazzuk. és a hibajel egyenletét állítsuk össze. levonva (8) a (7) -től: (9). A (9) egyenletből kiválasztjuk a jelet (10). A (10) megvalósításához a polinom Hurwitz-tulajdonsága szükséges. amely a mátrix megfelelő kiválasztásával biztosítható. Ez a választás azonban nem mindig lehetséges. Így léteznie kell egy mátrixnak. Hurwitz számára a polinomot. ami a feltételezésben nem szereplő további korlátozás. Mert. akkor (9) megvalósítható, és egy kiegészítő vezérlőjelet (11) alakítunk ki, és megkapjuk az objektum állapotvektorának egyenletét. Assertion 2. Hagyja, hogy a feltevések tartsanak, és van egy mátrix. amely biztosítja az átviteli függvény számlálójának stabilitását (8). Ezután a (4), (6), (8), (11) egyenletek által leírt dinamikus folyamatok vezérlik a célállapot (4) teljesítését.
-
példa
Megfontoljuk a stabilizációs problémát egy kontroll objektum számára, ahol a dinamikus folyamatokat az (1) - (3) egyenletek írják le. . . . . . A formában az ellenőrzési törvényt alkotjuk. Az 1. állítás feltételei teljesülnek. Az egyszerűség kedvéért az összes változó paraméter nulla értékű, és a következő szabályozó mátrixot kapjuk meg: a segédvezérlő művelet formában van. hol. . A vizsgált példában a következő kiegészítő ellenőrzési lépéseket kapjuk. Ezután megkapjuk a mátrixot a segédáramkörben
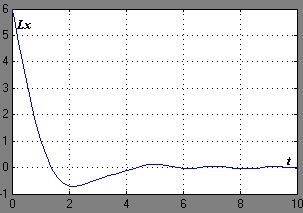
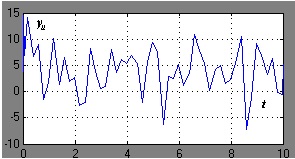
. megfelelő számokkal. Az 1. ábrán. Az 1. ábra bemutatja az ellenőrzési rendszer modellezésének eredményeit a következő kezdeti adatokkal: kezdeti feltételek. perturbáló hatások a bemeneten és. a kimeneti zaj véletlenszerű jel.
Ábra. 1. Átmeneti folyamatok a rendszerben véletlenszerű jel esetén Ebben az esetben a célállapot 8 másodperc elteltével kerül végrehajtásra.
A probléma az építési robusztus lineáris álló objektumot rendszer késések és korlátozás nélkül a vezérlő, amely képes ellensúlyozni a perturbáció tette a bemeneti és kimeneti rendszer, ahol a zavarok különböző. A tervezett vezérlőrendszer lehetővé teszi, hogy kompenzálják a zavarok hatását az ellenőrzött változókra meghatározott pontossággal, amint azt a példa is mutatja.
Alapvető kifejezések (automatikusan generált). Az ellenőrzési rendszer robusztus irányítási algoritmus külső zavar lineáris vezérlés, a maximális rangot nulla, egyenes robusztus irányítás, AM Tsykunov, megfigyelők külső zavarások tervezett ellenőrzési rendszer, a lineáris objektum Fizetési perturbáció mátrix mérete, a külső kör, a kezdeti mátrix, a kontroll lineáris tárgy, a mátrix hatékonyságát zavarások lineáris rendszerek, komplett, vezérlő jog mátrix kontroll lineáris objektumot.