Minimális tömbfák a betöltött grafikonok - stadopedia
A G = (X.A) gráfot betöltöttnek nevezzük. ha minden él (xi, xj) hossza (vagy súlya) meg van definiálva.
Legyen G egy csatlakoztatott grafikon. A minimális feszítőfa megépítésének feladata, hogy megtalálja a fát a feszítõ fák sorából, amelyhez a szélek hosszának összege minimális.
Adunk néhány tipikus esetet, amikor szükségessé válik egy gráf minimális feszítőfája létrehozása.
a) Meg kell csatlakoztatni n városok vasútvonalak (autó kormányzati utak, elektromos vezetékek, csővezetékek, hálózat, stb), hogy a teljes hossza a vonalak vagy a költség minimális lenne.
b) Olyan elektromos hálózatot kell létesíteni, amelyben a kapcsokat a legkevesebb hosszúságú vezetékekkel kell összekötni.
A minimális feszítőfa kialakításának problémája a következő algoritmussal megoldható.
3.2 algoritmus (Kruskal algoritmus).
1. lépés: A kezdeti értékek beállítása.
Bemutatjuk a G. gráf éleinek hosszának mátrixát.
2. lépés: Válassza ki a minimális hossz szélét a G gráfban. Konstruálja a G2 grafikont. Ez egy adott él és incidens csúcsból áll. Tegyük fel i = 2.
3. lépés Ha i = n. ahol n a gráf éleinek száma, akkor fejezze be a feladatot (a probléma megoldódik), ellenkező esetben lépjen a 4. lépésre.
4. lépés Construct a grafikon Gi +1, hozzátéve, hogy a grafikonon Gi új él mini-minimális hosszúságú, kiválasztott között a széleit a gráf amelyek mindegyike az eset, hogy néhány vertex Gi, és ezzel egyidejűleg az eset, hogy néhány csúcsa a gráf nem szerepel G. gi. Ezzel a peremmel együtt a Gi + 1-ben és a Gi-ban nem szereplő incidens csúcshoz tartoznak. Assign i: = i + 1, és menjen a 3. lépésre.
Megtaláljuk a minimális feszítőfát a 3. ábrán látható gráfra. 3.14.
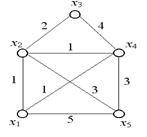
1. lépés: A kezdeti értékek beállítása.
Bevezetjük a C szélek hosszának mátrixát:
2. lépés: Válasszon egy minimális élszélességet. Egy él minimális hossza egy. Három ilyen széle van: (x1. X2), (x1. X4), (x2. X4). Ebben az esetben bármelyiket megteheti. Vegyük (x1. X2). Készítsük el a G2 grafikont. amely egy adott perem és incidens csúcsokból áll, x1 és x2. Az i = 2 értéket állítjuk be.
3. lépés. Mivel n = 5, akkor i ¹ n. így folytassa a 4. lépéssel.
3. lépés: i ¹ n. így folytassa a 4. lépéssel.
3. lépés: i ¹ n. így folytassa a 4. lépéssel.
3. lépés: i = n. akkor a G5 a szükséges minimális feszítőfa. Az élek teljes hossza 1 + 1 + 2 + 3 = 7.
A minimális feszítőfa kialakításának folyamatát az 1. ábrán mutatjuk be. 3.15.
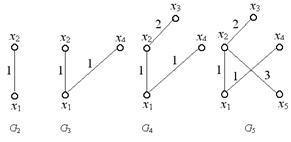
TÉMA 4. FUNKCIÓS BÚTOROK