Az exponenciális simítás módszerén alapuló előrejelzés
Az extrapoláció a tudományos kutatás egyik módja, amely a múltbeli és a jelenlegi tendenciák, minták, az előrejelző objektum jövőbeli fejlődéséhez való kapcsolódásokon alapul. Az extrapolációs módszerek közé tartozik a mozgó átlag módszer, az exponenciális simítás módszere és a legkisebb négyzetek módszere.
Az exponenciális simítás módszere a leghatékonyabb a középtávú előrejelzések kidolgozása során. Elfogadható, ha csak egy előre megjósolt időt előre jelez. Fő előnyei a számítási eljárás egyszerűsége és a kezdeti információk súlyának figyelembe vétele. Az exponenciális simítás módszerének működőképessége:
ahol t az előrejelzést megelőző időszak; t + 1 az előrejelzési időszak; Ut + 1 - előre jelzett indikátor; # 945; - simító paraméter; Vt - az előrejelzést megelőző időszak alatt a vizsgált mutató tényleges értéke; Ut - az előrejelzést megelőző időszak exponenciálisan súlyozott átlaga.
Ennek a módszernek a megjóslásakor két nehézség van:
- válassza ki a simítási paraméter értékét # 945 ;;
- az eredeti Uo érték meghatározása.
Az értéktől # 945; Ez attól függ. milyen gyorsan csökken a korábbi megfigyelések hatásának súlya. Annál többet # 945; annál kevésbé befolyásolja az előző évek hatása. Ha az érték # 945; közel az egységhez, akkor ez az előrejelzéshez vezet, amelyet főként az utolsó megfigyelések befolyásolnak. Ha az érték # 945; közel nulla, akkor azoknak a súlyoknak a száma, amelyekkel az idősorok szintjeit lemérjük, lassan csökken; az előrejelzésben az összes (vagy csaknem minden) múltbeli megfigyelést figyelembe veszik.
Így ha bizalom áll fenn, hogy az előrejelzés alapjául szolgáló kezdeti feltételek megbízhatóak, a simítási paraméterek (# 945; → 0) kis mennyiségét kell használni. Ha az anti-aliasing paraméter kicsi, a vizsgált függvény átlagos múltbeli szintek átlagaként viselkedik. Ha nincs elég bizalom az előrejelzés kezdeti feltételeiben, akkor nagyobb értéket kell alkalmazni # 945, ami az előrejelzés számlájához vezet majd, alapvetően az utolsó felügyelet hatása miatt.
ahol n a kiegyenlítés intervallumát bejutó megfigyelések száma.
Az Uo (exponenciálisan súlyozott középérték) kiválasztásának problémája az alábbi módokon oldható meg:
- ha bizonyíték van a jelenség fejlődésére a múltban, akkor használhatjuk a számtani átlagot, és egyenlővé tehetjük Uo-val;
- ha nincs ilyen információ, akkor a V1 predikciós alap kezdeti értékét Uo-ként használjuk.
Szakértői becsléseket is használhat.
Megjegyezzük, hogy a gazdasági idősorok tanulmányozása és a gazdasági folyamatok előrejelzése során az exponenciális simítás módszere nem mindig működik. Ez annak köszönhető, hogy a gazdasági idősorok túl rövidek (15-20 megfigyelés), és abban az esetben, ha a növekedés és a növekedés üteme magas, ez a módszer nem "kezeli" az összes változást.
Példa az exponenciális simítás módszerére az előrejelzés kidolgozásához
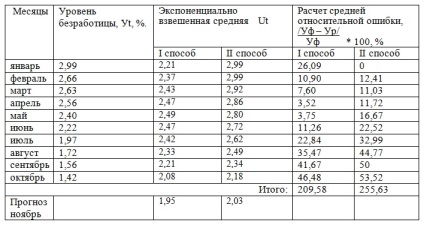
A feladat. A régióban a munkanélküliségi arányt jellemző adatok vannak,%
Megoldás exponenciális simítás módszerével
1) Határozza meg a simítási paraméter értékét a következő képlet segítségével:
ahol n a kiegyenlítés intervallumát bejutó megfigyelések száma. # 945; = 2 / (10 + 1) = 0,2
2) Az Uo kezdeti értékét két módon határozzuk meg:
I módszer (aritmetikai átlag) Uo = (2,99 + 2,66 + 2,63 + 2,56 + 2,40 + 2,22 + 1,97 + 1,72 + 1,56 + 1,42) / 10 = 22,13 / 10 = 2,21
II módszer (az előrejelzési bázis első értéke) Uo = 2.99
3) Számítsa ki az exponenciálisan súlyozott átlagot minden egyes periódusra a képlet segítségével
ahol t az előrejelzést megelőző időszak; t + 1 az előrejelzési időszak; Ut + 1 - előre jelzett indikátor; # 945; - simító paraméter; Vt - az előrejelzést megelőző időszak alatt a vizsgált mutató tényleges értéke; Ut - az előrejelzést megelőző időszak exponenciálisan súlyozott átlaga.