A matematika kezdeti tanfolyamának fő tartalmi elemei, kapcsolatuk
Az iskola I.-IV. Évfolyamaiban tanult matematika kezdeti tanfolyama szerves részét képezi a matematika tanfolyamának. Ez azt jelenti, hogy a V-X osztályok matematikai kurzusa a kezdeti tanfolyam folytatása, és a kezdeti tanfolyam az alapja. Ennek megfelelően a matematika kezdeti kurzusa magában foglalja a nem negatív egész számok és az alapvető mennyiségek, az algebrai elemek és a geometria elemeit.
A matematika kezdeti tanfolyamának saját építési jellemzői vannak.
Egy ilyen kapcsolat lehetõvé teszi egyrészt, hogy a gyermekeket az algebra és a geometria eszméire vezessék be, másrészt pedig a fiatalabb iskolai gyerekek számára magasabb szintû aritmetikai tudást érjenek el.
Az aritmetikai anyag koncentrikusan kerül bevezetésre. Először vizsgálták számozás első tíz számok, amelyek nem tartoznak a tizedes feldarabolás, beírt számok rögzítésére ezeket a számokat, tanulmányozzuk az intézkedés az összeadás és kivonás. Ezután megvizsgáljuk a sorszám, 100, ismertetik a koncepció kisülés elvén rögzítésihelyzet számok, amelyekre tizedes feldarabolása, tanulmányozta az összeadás és kivonás kétjegyű számokat két új aritmetikai műveletek: szorzás, osztás. Ezután megvizsgáljuk a sorszám belül 1000. Foglalkozik három kategóriában (egység, tíz, száz) alapját képező, a számozás több szám, generalizált ismerete számtani bevezetett technikák írásbeli összeadás és kivonás. Végül tanulmányozzuk a számozás több számjegyű számokkal, megbeszéljük a koncepció osztály, általános ismeretek az elvet a partra értéke számjegyet írt számítások vizsgálták. Így a tanfolyam kiemeli négy koncentrációjával: egy tucat, száz, ezer, nagy számok. Ugyanakkor, és szoros kapcsolatban áll a számozás és a számtani tanulmányozták más kérdések: értékek, frakciók, algebrai és geometriai anyag.
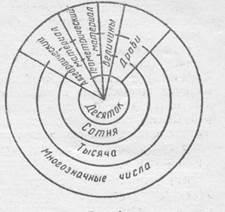
Az anyag elrendezését az ábrán vázlatosan mutatjuk be.
Az elosztást a funkciókról concenters magyarázta a tízes számrendszer és számítási módszerek: minden koncentrációban feltárja új kapcsolatos kérdések a számrendszer és számtani. A tapasztalat azt mutatja, a koncentrikus elrendezése az anyag megfelel a képességeinek fiatalabb diákok: Matematika oktatás kezdődik egy kis területen a számok rendelkezésre a gyermekek és a jól ismert, hogy az iskolába; a számok ezen területe fokozatosan bővül, és új koncepciókat fokozatosan bevezetnek; Ilyen módon épülnek fel a rendszeres ismétlés, és egyidejűleg a tanulmányozott elmélyítés, mivel a korábban szerzett tudást, készségeket és készségeket egy új számtartományban alkalmazzák. Mindez hozzájárul a tanfolyam jobb elsajátításához.
A kurzusban matematikai fogalmak, tulajdonságok, szabályszerűségek tárulnak fel. Ez nemcsak a számtani, algebrai és geometriai anyag összefüggése, hanem az ún. Belső összefüggések a kurzus, tulajdonságok, törvények különböző fogalmai között. Így a számtani műveletek tanulmányozása során feltárják azok tulajdonságait, kapcsolatait és függéseit komponenseik és eredményeik között. Ez lehetővé teszi, hogy mélyebben feltárják a számtani műveletek fogalmát, gazdagítják a gyermekeket funkcionális ábrázolással. Ez a szerkezeti kialakítás egy mélyebb asszimilációja során, a diákok szerez nemcsak az egyes kérdések során, de ugyanakkor és a köztük lévő kapcsolatok.
A számtani anyag magában foglalja a nem negatív egész számok számát és a számtani műveletek számát, a mennyiségekre vonatkozó információkat, azok mérését és műveleteit, a frakciók fogalmát.
Ennek az anyagnak a tanulmányozása arra kell, hogy vezesse a diákokat, hogy elsajátítsák a matematikai fogalmak rendszerét, valamint hogy erős és tudatos készségeket és készségeket elsajátítsanak.
A nulla számot a kezdeti kurzus során az üres sorok kvantitatív jellemzőjeként kezelik. Felvételét az alaptanfolyam a matematika és a számok nulla tágul numerikus tartományok és teremtsenek megfelelő feltételeket a diákok mastering terület nem negatív egész. A nulla szám és a számjegy az I. osztályba kerül. Először is, a nulla tekinthető ez a szám azt jelzi, hogy a mérés megkezdéséhez sorban, majd adja meg a nullát kivonva típusok: 2-2, 3-3, ami megfelel a helyes értelmezése a lényege ennek az új számot mennyiségi jellemzőit üres osztályt készletek. Következő, nulla szolgál az első szakaszban cselekvési összetevője: 5 + 0, 0 + 9, 8-0, 0 + 0, O-O, és a tanulmány a fellépés szorzási és osztási (II osztály) komponenseként ezen intézkedések: 0-4, 3 -0, 0-0, 0: 4. Itt mérlegeljük a nullával való elosztás lehetetlenségét is. A nulla szám jelöli hiányában egység a kisülés a rekordszámú (70, 30,000, 204).
A kezdeti osztályokban a frakció vizuális ábrázolását adjuk meg. A második osztályban a részvény fogalmát az egész egy részének egyike (kör, zsinegdarab) vezeti be, a részvények nyilvántartását adják meg. Mivel a részvény fogalmának lényegét nagyon világosan derítik fel a problémák számának megoldásában, hogy egy szám törtrészét és számát töredékével találják meg, ezeket a problémákat a második osztályban vizsgált kurzus tartalmazza. A III frakciót vezetnek, mint egy több frakcióra, frakciók felvétel, konvertáló, és a frakciókat képest a probléma találni a frakció.
A számrendszer fogalmát a tanfolyam fokozatos koncentrálásával fedezzük fel, amikor a természetes számok számozását és a számelméleti műveleteket tanulmányozzuk. Ugyanakkor a kategória, az osztály, a számjegy és az osztályegység fogalma, a számjegyszám, ahogy már jeleztük, a koncentrációtól a koncentrációig, vagyis az új osztályoktól és osztályoktól, fokozatosan bevezetik nevüket, így az oktatás, a név, számok rögzítése és olvasása, tizedes összetétele.
A számtani tevékenység központi szerepet tölt be a matematika kezdeti szakaszában. Ez egy összetett és sokrétű kérdés. Ez magában foglalja a nyilvánosságra hozatala egy bizonyos értelemben aritmetikai műveletek, tulajdonságok, tevékenységek, kapcsolatok és függőségek a komponensek között, és az eredményeket a cselekvés és cselekvések között, valamint a kialakulását számítástechnikai ismeretek, képes megoldani a számtani problémákat.
Mint más matematikai fogalmak, minden aritmetikai művelet ismertet konkrét módon a folyamat a műveletek szett kívül - alapján az unió működését készletek nélkül közös elemek kivonás - a művelet alapján egy részének eltávolításával a beállított (részhalmaza), szorzás - a művelet alapján kombinálásával állítja, hogy azonos számú és osztály - a művelet alapján beállított particionálás egy több diszjunkt ravnochislennyh. Ez a megközelítés lehetővé teszi számunkra, hogy hivatkozhat a tapasztalat a gyermekek és hozzon létre egy vizuális keretet generált tudás. Egyidejűleg a megnyitása a konkrét jelentését minden aritmetikai művelet kerül beillesztésre a megfelelő szimbólumok (a védjegy) és terminológia: a művelet nevét, a nevét, a komponensek és az eredményeket az intézkedés. Itt művelet kezdődik a fogalom egy matematikai kifejezés, először azt a legegyszerűbb kifejezése a formában: 7 + 3 és később bonyolultabb formában 9- (2 + 3).
A matematika kezdeti kurzusa számos aritmetikai művelet tulajdonságait tartalmazza. Ez kommutatív összeadás és a szorzás tulajdon tulajdonságait kívül az összeg, kivonva száma az összeg hozzáadásával összeget a számot, kivonva száma adalék mennyisége az összegével, levonva az összeg összegének szorzata az összeg és az összeg a számot, az összeg osztva száma, szorozza a számot a terméken, a számot a termékre osztja.
Mindegyik tulajdonságot a készletek vagy több számok gyakorlati műveletei alapján adják meg, aminek következtében a diákoknak általánosságba kell kerülniük. A tanfolyam tulajdonságainak asszimilálására speciális gyakorlatok rendszerét biztosítják, de a tulajdonságok fő alkalmazási területe a számítógépes technikák alapján történő közzététel. Például már az I. osztályban, miután megvizsgáltuk az addíció elmozdulási tulajdonságát, bemutatjuk a summandumok permutációját a következő esetekben: 2 + 6; az 54-20. esetet megelőzően megfontolják a szám kivonásának különböző módjait az összegből, amely alapján a számítási módszer feltárul:
54-20 = (50 + 4) -20 = (50-20) +4 = 34.
Ennek alapján a konkrét jelentése aritmetikai műveletek, azok tulajdonságait, kapcsolatok és függőségek között a komponensek és a műveletek eredményét, valamint a tizedes részét számok feltárt technikák szóbeli és írásbeli számításokat. Ez a megközelítés a tanulmány a számítógépes technikák segítségével, egyrészt, a formáció a tudatos és készségek, a hallgatók képesek lesznek, hogy minden, a számítógépes technika és másrészt, az ilyen rendszer jobban felszívódik a műveletek tulajdonságainak, és egyéb problémák a kurzus.
Ezzel párhuzamosan a tanulmány tulajdonságainak aritmetikai műveletek és a megfelelő módszerek számítások nyilvánosságra alapján a műveletek meghatározza vagy kapcsolatszáma az alkatrészek között, és az eredményeket a számtani műveletek (például, ha az összeg az elvesz egy a feltételek, akkor kap egy másik kifejezés) végzett megfigyelések változások aritmetikai eredmények attól függően, változások az egyik komponens (például, ha az egyik a feltételeket, hogy növelje az egységek száma, és a másik változatlan marad, az összeg növekedni fog kemping az azonos számú egység).
A matematika kezdeti kurzusában a gyakorlati rendszer célja, hogy fejlessze a hallgatók számítástechnikai készségeit. Ez a képzés gyakorlatok különböző jellegű: a határozat egyedi példák, kitöltve a táblázatok, a helyettesítését számértékek betűk és megtalálni az értékeket a kifejezést nyert. A formáció a szakértelmet biztosít különböző fokú automatizáltság, mint például összeadást készségek és szorzótábla az esetek és a hozzájuk való visszatérés kivonás és osztás esetet be kell jelenteni, hogy a teljes automatizmus (például a diákok kell gyorsan és pontosan reprodukálni, hogy a 3 + 8 = 11, 7x6 = 42, 12-5 = 7, 56: 8 = 7). Automatizált és egyedi műveletek végrehajtása; így például, hozzáadásával a számok 18 és 7 gyorsan végrehajtott lépéseket tartalmazza: 8 + 7 = 15, 10 + 15 = 25, vagy 7 + 5 = 2, 18 + 2 20 = 20 + 5 = 25.
Mindezeket a számokat a számtani tevékenységekkel kapcsolatban szoros kapcsolatban kell tartani egymással.
Az algebra számtani elemeinek elemzésével kapcsolatban konkrét alapon bemutatják az egyenlőség, az egyenlőtlenség, az egyenlet, a változó fogalmát.
Az első osztálytól kezdve számszerű egyenlőtlenségeket és egyenlőtlenségeket kell figyelembe venni
3 = 3, 5 = 1 + 4, 3<4, 7+2>7, 9-3<9-2 и т. п. Их изучение непосредственно связывается с изучением арифметического материала и помогает более глубоко раскрыть его. Здесь же рассматриваются уравнения сначала вида: х + 6 = 9, 10—х=2.. а позднее, начиная соIIкласса, вида: (48 ++х)— 24 = 36. Решение уравнений выполняется на основе связи между компонентами и результатами арифметических действий, а также способом подбора. Наряду с решением уравнений ведется обучение решению задач с помощью составления уравнений. ВоIIклассе вводится буква как символ для обозначения переменной. В связи с этим рассматриваются выражения с переменной(а + Ь, 20 —с и др.) и неравенства с переменной 9 —с<5), значения переменной в которых находится способом подбора.
A geometriai anyag elsősorban a legegyszerűbb geometriai alakok ismeretét és az iskoláskorú térbeli ábrázolások fejlesztését szolgálja. Ezért a kezdeti során matematika, kezdve I osztályba tartoznak geometriai formák: egyenes, görbe és szaggatott vonalakat, pont, vonal szegmens, a sokszögek (háromszög, négyszög.) És az elemek (vertex, az oldalán, sarkok), merőleges téglalap ( négyzet), kör, kör, középpont és sugara. A hallgatóknak meg kell tanulniuk megkülönböztetni ezeket a számokat, felhívni őket, és egyszerűen megmunkálni a kockás papírra. Ezen túlmenően, rendelkezniük kell a képességét, hogy megtalálják a hossza a szegmens (I osztály), a hossza a vonallánc és sokszög kerülete (II osztály), a terület a geometriai formák (III osztály) .Kurs matematika nyújt a különböző feladatok egy geometrikus jellegű, amelyek célja a kialakulását térbeli ábrázolások tanulók. A geometria minden kérdése vizuálisan jelenik meg.
Az aritmetikai, algebrai és geometriai anyagokkal való szoros összefüggésben kiderül a nagyság nagysága és mennyiségi mérete. Megismerése olyan értékeket, mint hosszúság, a tömeg, az idő, a kapacitás, a területen, a mértékegységek, és a mérési értékek történik virtuálisan, és szorosan kapcsolódik a kialakulását a fogalmak, a tízes számrendszerben, és aritmetikai, valamint a kialakulását a koncepció egy geometriai alakzat. Ebből a kapcsolatból képessé válik a vizuális képekre támaszkodva a tanulás a gyermekek gyakorlati tevékenységével.