DirectX virtuális kamera direct3d-ben

Figyelem! Ez az oldal nem frissül. Új verzió: shatalov.su

Előzetes leckék:
1. Coordinate spaces. Go.
2. A koordináta terek átalakítása. Go.

További leckék
1. Mozgás térben és forgatás egy tetszőleges egyenes vonal körül. Go.

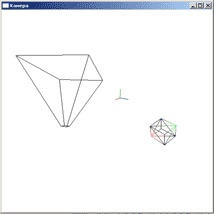
Ma megnézzük a virtuális kamera eszközét. Kezdjük a képet.

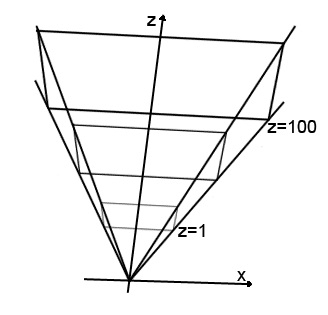
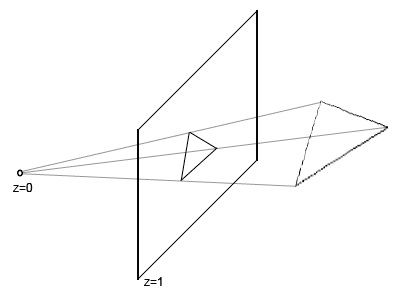
Az ábrán látható a kamera koordinátarésze. A fényképezőgép iránya ("nézet") mindig egybeesik a z tengely pozitív irányával, és maga a fényképezőgép a kiindulóponton helyezkedik el.

Az ábrán ábrázolt piramis belső térrésze a virtuális világ azon része, amelyet a felhasználó látni fog.

Figyeld meg a három repülőgépet. Az első a z tengely mentén 1-es távolságban helyezkedik el. Ez a közel sík. Amit a játékos előtt látni nem fog látni. Ebben az esetben a z értéke egyenlő egy, de általában véve lehet bármely. A közel síkban van egy hiba a grafika megjelenítésében. Ez a hiba elsősorban lövőknél jelentkezik (a kamera nagy szabadsága miatt). Ha túl közel van az objektumhoz, lehet "belül". A legutóbbi játékok közül ez a hiba különösen nyilvánvaló volt a bal 4 halottban: amikor egy zombi tömeg összegyűlt a lejátszóra, nagyon gyakran lehetett más karakterek között is belenézni.

A z tengely mentén 100 egységnyi távolságban elhelyezkedő síkot messzire hívják. Ismét az érték tetszőleges lehet. A felhasználó soha nem fog látni az ezen a síkon kívül eső objektumokat.

Hat sík, amelyek a felhasználó által látott helyet határolják, a leágazási síkok: bal felső jobb alsó és közeli.

A közeli és távolsági sík között elhelyezkedő sík. A jövőben ez a sík z = 1-ben helyezkedik el, azaz. ez egybeesik a közeli. Itt szétválasztottam a közeli és a vetítési síkot, hogy megmutassam, hogy ez még mindig nem ugyanaz. A vetítési sík a koordináták utolsó átalakulására szolgál: az átalakulás a kamera háromdimenziós téréből a kétdimenziós térbe.

A vetítési síknak köszönhetően a felhasználó látni fogja a virtuális világot. Valójában ez a sík az, amit a felhasználó lát. A vetítési sík közvetlenül kapcsolódik olyan fogalmakhoz, mint a fő / háttér pufferek, a programablak és a felhasználó képernyője. Mindezek a fogalmak négyszögletes képnek tekinthetők, amelyet a számítógép memóriájában egy sor számsor képvisel.

A koordináta háromdimenziós világból a projekciós síkba történő átalakítása a legösszetettebb azok közül, amelyeket eddig tanulmányoztunk.

Nézet / látómező

A fenti ábrán a vetítési sík szélessége (és ezért a felhasználó által látott kép) szélessége nagyobb, mint a magasság. A vetítési sík szélességét és magasságát szögek alkalmazásával határozzák meg. Ezen szögeknél különböző nevek találhatók: a látómező vagy a megtekintési terület. Angolul - látóterek.

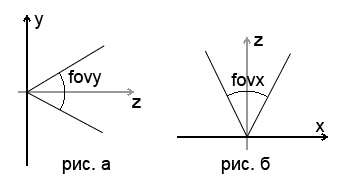
A megtekintési zónákat két szög határozza meg. Nevezzük: fovx - vízszintes megtekintési terület, fovy - függőleges megtekintési terület. Részletek a megtekintési területeken: lent.

Z-puffer / w-puffer / mélységi puffer (z-puffer / w-puffer / mélységi puffer)

Nézzük meg a képet, amely két háromszöget ábrázol: 25 és 50 a kamerából. Az a) ábra mutatja a háromszögek helyét a térben (felülnézet), és a (b) ábrán láthatja a végleges képet:

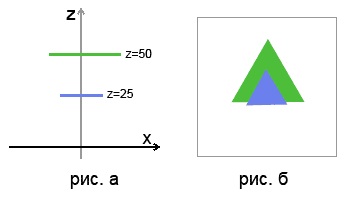
Amint azt feltételezed, a képet a legtávolabbi elemektől a legközelebbihez kell húzni. A nyilvánvaló megoldás: kiszámítja a távolságot a kiindulástól (a fényképezőgéptől) minden objektumhoz, majd hasonlítsa össze. A számítógépes grafikáknál kissé fejlettebb mechanizmust használnak. Ez a mechanizmus több elnevezéssel rendelkezik: z-puffer, w-puffer, mélységpuffer. Az z-puffer nagysága az elemek számával megegyezik a háttér és a fő pufferek méretével. A fényképezőgéphez legközelebb eső objektum z-komponense a z-pufferben tárolódik. Ebben a példában, ahol a kék háromszög átfedi a zöld háromszöget, a kék z koordinátái kerülnek a mélységi pufferbe. A z-puffert részletesebben egy külön leckében tárgyaljuk.

Ortográfiai / párhuzamos vetület

Az a művelet, amelynél a térméretesség csökken (háromdimenziós tér van, kétdimenziós térré vált), egy vetületnek nevezik. Először is érdeklődünk egy perspektivikus kivetítés iránt, de párhuzamos (párhuzamos vagy ortográfiai vetülettel) ismerkedni fogunk.

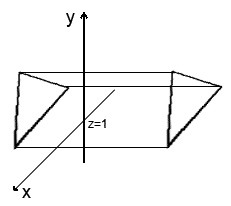
A párhuzamos vetület kiszámításához elegendő az extra koordináta eldobása. Ha van egy pont az űrben [3 3 3], akkor amikor a vetület párhuzamos a z = 1 síkkal, akkor a [3 3 1] pontra kerül.

Perspektív vetítés a vetítési síkon

Ebben a típusú vetületben minden vonal egy ponton konvergál. Így van elképzelésünk. És perspektivikus kivetítés segítségével az összes játék "megjelenése" modellezés.

Hasonlítsuk össze ezt a figura a minta mutatja a homogén koordináták az előző leckét. Váltáshoz kétdimenziós, az első két alkatrészt kell osztani a vektorok harmadik háromdimenziós térben: [x / z y / z z / z] = [x / z y / z 1].

Ahogy fent írtam, a vetületi sík bárhol elhelyezhető a közelben és messze. A vetítési síkot mindig z = 1-re tesszük, de ebben a leckében más lehetőségeket is megvizsgálunk. Nézzük meg a képet:

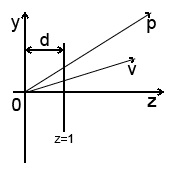
A vetületi síknak a származástól való távolságát d jelöli. Két esetet vizsgálunk: d = 1 és d = 5. Fontos pont: az összes vektor harmadik komponense a vetület után egyenlő legyen a d-val - minden pont azonos síkban helyezkedik el z = d. Ezt úgy érhetjük el, hogy a vektor minden összetevőjét megszorozzuk: d: [xd / z yd / z zd / z]. Ha d = 1, akkor kapjuk: [x / z y / z 1], akkor ezt a képletet használtuk homogén koordináták transzformálására.

Ha most otodvinem projekciós síkon, hogy a pont a Z = 5 (sootvtestvenno d = 5), kapjuk: [xd / z km / z zd / z] = [5x / z 5Y / z 5]. Az utóbbi általános képletű projektek minden vektor egyetlen síkban, ahol d = 5.

Itt van egy kis probléma. Az előző képlet háromdimenziós vektorokkal működik. De egyetértettünk abban, hogy négydimenziós vektorokat használunk. A negyedik komponens ebben az esetben egyszerűen eldobható. De ezt nem fogjuk megtenni, mivel használata bizonyos speciális képességeket biztosít, amelyeket megvitatunk.

Szükséges megtalálni a harmadik és a negyedik komponens közös osztóját, amikor a harmadik összetevőre oszlik, d értéke marad, és a negyedikben. Ez a partíció d / z. Most a szokásos vektornál [x y z 1] meg kell szerezni egy vektort, amely készen áll a vetítésre (osztás) [x y z z / d]. Ezt a transzformációs mátrix alkalmazásával végezzük (ellenőrizzük az eredményt, ha vektort megszorozunk az adott mátrixon):

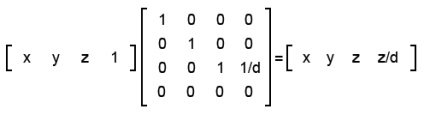
Az utolsó átalakulás nem egy vetület. Itt csak az összes vektort hozzuk létre a szükséges formához. Emlékeztetlek, hogy a vetítési síkot d = 1-ben tesszük, így a vektorok így fognak kinézni: [x y z z].

Perspektivikus transzformáció mátrixa

Megvizsgáljuk a DirectX-ben használt perspektivikus transzformációs mátrixot:

Most már tudjuk, hogy mi a _34 elem. Azt is tudjuk, hogy az _11 és _22 elemek vízszintesen és függőlegesen skálázzák a képet. Lássuk, mi van pontosan az xScale és yScale nevek mögött.

Ezek a változók a megtekintési zónáktól függenek, amelyekről fent beszéltünk. Ezeknek a sarkoknak a növelésével vagy csökkentésével a kép méretarányos (méretarányos vagy nagyított) - a vetítési sík méretének és képarányának megváltoztatása. A zoom mechanizmus távolról hasonlít a fényképezőgépek / kamerák zoomolására - az elv nagyon hasonlít. Tekintsük a képet:

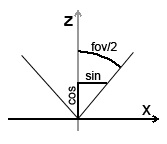
A szöget két részre osztjuk, és csak a felét veszik figyelembe. Amit itt látunk: növeljük a fov / 2 szöget (és ennek megfelelően a szög fov), növeljük a büszögszöget és csökkentjük cos értékét. Ez a vetületi sík növekedéséhez, és ennek következtében a vetített tárgyak csökkenéséhez vezet. Az ideális szög a fov / 2 = P / 4. Emlékszem, hogy a szög P / 4 radianban 45 fok. Ebben az esetben a fov egyenlő lesz 90 fokkal. Mi a jó 45 fokos szögben? Ebben az esetben nincs skálázás, és cos (P / 4) / sin (P / 4) = 1.

Most a kép függőlegesen (vízszintesen) méretezhető, a látóterület felének szinuszával és koszinuszával (a C + + cotangent funkciót cot-nak nevezik):

A DirectX-ben csak a függőleges megtekintési területet (FOVY) használják, és a vízszintes méretezés függ a függőleges megtekintési területtől és a képaránytól.

Emlékeztetlek arra, hogy a programunkban lévő ablak 500x500. Képarány: 1 - 1. Ezért a változók egyenlőek lesznek: xScale = 1, yScale = 1.

A standard monitor / TV képaránya: 4: 3. Ez az arány megfelel a képernyő felbontásának: 640x480, 800x600, 1600x1200. A teljes képernyős módot még nem érjük hozzá, de megváltoztathatjuk a programablak méretét. Megváltoztathatja az ablakméretet (a jelenlegi paraméterekben), például 640X480-ra. De az összes tárgy nem nyúlik meg (a négyzetek téglalap alakúnak tűnnek), ne felejtsd el megváltoztatni a megfelelő változókat a vetítési mátrixban.

Szinte elfelejtettem, az xScale fórum a DirectX-ben:

A képarányok egyszerűen: 1/1, 4/3, 16/9 - ez a szabványtól függ.

Az perspektivikus transzformációs mátrix elemeinek _33, _34 céljainak megismerése továbbra is fennáll. ZF - Z-koordinátája a távoli síkban (F ar - eddig) és Zn - Z-koordinátája a közeli (n fül - szoros). Megjegyezzük, hogy az elem _43 = _33 * -zn.

A legegyszerűbb módja annak, hogy megértsük, mi a pontosan ezek a képletek. A standard vektort [x y z w] szorozzuk meg a fenti mátrixon. Azt javaslom, hogy ezt egy papírlapot és egy ceruzát vegye be (remélem, emlékszel arra, hogyan szaporodhatod meg a két mátrixot). A vektor komponensei a következő alakban vannak.

Végezzük vetületi transzformáció (osztani az összes elem a negyedik komponenst, ahol feltételezzük, hogy d = 1, és w = 1):

Ennek eredményeképpen egy olyan vektort kaptunk, amelyik a következő formát tartalmazza:

Most, ha meg a konkrét értékeket zf és zn, majd keresse meg a következő (pozitív értékek): ha a vektor a közeli sík, a z-komponens átalakítás után lesz kevesebb, mint nulla, ha a vektor található, a távoli gépen, a z-komponens nagyobb lesz egységet.

Nem tesz különbséget, hogy hol található a közeli és távoli sík: zn = 1, zf = zn = 10 vagy 10, és a ZF = 100 (vagy bármely más érték) - alakítása után a látható terület lesz található az intervallum nulla vagy egy, a befogadó.

Erre a célra, és a célja, hogy elemei képletű _33, _34 projekciós mátrix - kiáll a proximális és a disztális síkban a [0, 1]. Ezt ellenőrizze, ha kiszámítja a vektorok értékeit a zn, zf (igen, egy darab papírra) meghatározott értékekre.

Arkanoid

fényképezőgép
sejteket
sprite