A rotációs mozgás dinamikájának alapvető egyenlete
Képviselnek szilárd test, amely egy forgáspont körül rögzített tengely miatt, hogy az erő (H) egy váll erők (m). Ahol a test mozog szögsebességgel (rad / s), és megszerzi szöggyorsulás (rad / s2). A szögsebesség azt a szöget jelenti, amelyhez a test a tengely körül egységenként forgott. Míg az előremenetben a tömeg a tehetetlenség mértéke. kiszámításakor forgómozgást evégett egy tehetetlenségi nyomatéka, amely jellemzi a tömegeloszlás a test térfogatának (itt r - a leíró függvény pontok sűrűsége a test és a távolság a forgástengely; m - tömege minden egyes pont, V - a térfogata a szervezetben). A tehetetlenségi nyomaték kg-ban m 2.
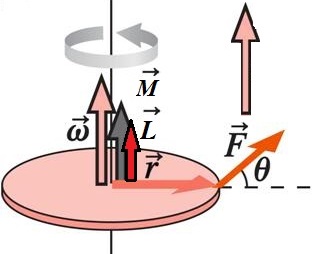
A rotációs mozgás dinamikájának alapvető egyenlete
A mozgás okának és a hatásnak (a szögsebesség megszerzésének) összefüggésében a rotációs mozgás leírásához használja a rotációs mozgás dinamikájának alapegyenletét:
Itt - az erõ pillanatában, jellemezve, hogy az erõ milyen intenzíven hat a testre.
Meg kell jegyeznünk, hogy valójában az M erő és a szögsebesség pillanata vektor mennyiségek. A forgás dinamikájának egyenlete azonban pontosan az abszolút, skaláris értékeket köti össze.
Ha a test tehetetlenségi nyomatéka időben változhat (például ütőpréseknél a folyadék a lendkerék tömegének belsejébe kerül), a forgási mozgás dinamikájának egyenlete általánosabb formát ölt:
A termék = L a test minden pontjának szögsebessége a forgástengelyhez viszonyítva. Néha ezt a "forgás lendületét" is nevezik.
Példák a problémamegoldásra
A 20 cm átmérőjű és 5 kg tömegű golyó a szimmetria tengelye körül mozog. Ezt a mozgást törvény írja le. rad / s, rad / s. Keresse meg az erők pillanatát a tengelyhez képest c időpontban.
A gömb sugarának fele az átmérője: R = 0,1 m
Számítjuk ki a tehetetlenség pillanatát (a különböző értékek tehetetlenségi nyomatéka a referencia irodalomban található):
Az erők pillanatát a rotációs dinamika egyenlete alapján találjuk meg:
A lendkeréknek 245 kg • m 2 tehetetlenségi nyomatéka van és 20 s -1 frekvencián forog. Időnként a fékerőt ráhelyezték, és 1 perc elteltével a lendkerék megállt. A lendkerék sugara 0,2 m. Számolja ki a fékerő pillanatának nagyságát és a lendkerék által teljes fordulatszámot, mielőtt leáll.
Csak egy erő működik a lendkeréken, ami megteremti a nyomatéknyomatékot - a súrlódás erejét. Ezért a rotációs mozgás dinamikájának egyenlete a következőképpen alakul:
Mivel a lendkerék egyenletesen lassul, megtaláljuk az összetevőt:
Ezt a kifejezést a rotációs mozgás dinamikájának egyenletében helyettesítjük:
A fordulatok teljes számát úgy kapjuk meg, hogy megszorozzuk a lendkerék átlagos forgási frekvenciáját a fékezési idő alatt. Az átlagos sebesség a számtani átlag:
A fordulatszám teljes száma: