A gömbölyű bolygón a póluson a testtömeg 3-szorosa az egyenlítő testtömegének
Feladat állapota:
A gömbölyű bolygón a póluson a testtömeg 3-szorosa az egyenlítő testtömegének. Határozzuk meg a bolygó forgási idejét, ha az átlagos sűrűsége 2300 kg / m 3.
Task 2.5.9 a "Feladatok gyűjteménye az UGNTU fizikájának bejárati vizsgáinak felkészítésére"
\ (P_n = 3P_e \), \ (\ rho = 2300 \) kg / m 3. \ (T -
A probléma megoldása:
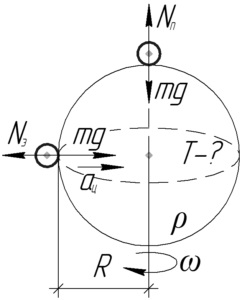
Az Egyenlõben levõ test elforgatja a bolygót, leírva egy kör sugarát (R \) (a bõr sugara). A második Newton törvényét erre a testre a következő formában kell megírni:
A póluson lévő test a tengelye körül forog, mert a bolygó tengelye átjut a test közepén. Mivel a bolygó elfordul, egy nulla sugarú kört fog leírni, akkor a centripetális gyorsulás nem jár. Newton első törvénye ennek a testnek ebben a formában lesz írva:
A következő rendszert kapjuk:
Figyelembe véve (1):
Mivel a (P_n = 3P_e \) hipotézis szerint, majd a rendszer alsó egyenlőségét a felsőbbre osztva, a következőket kapjuk:
A sűrűség \ (\ rho \) a sűrűség \ (g \) gyorsulását fejezi ki a bolygó felszínén. Ehhez a fogalommeghatározás képletét írjuk:
A bolygó tömegét a térfogat szerinti sűrűség terméke alapján találjuk meg, és a sugár sugarait kifejezzük, mivel a bolygó gömbölyű.
\ [M = \ rho \ cdot V = \ frac \ pi \ rho \]
Most fejezzük ki a centripetális gyorsulást \ (a_it) a forgási időn. Ehhez a centripetális gyorsulás meghatározására szolgáló képletet írjuk le a forgás szögsebessége és a forgás szögsebessége és a bolygó forradalmi időszaka közötti összefüggési képlet alapján:
A (3) és (4) kifejezést a (2) egyenletbe helyezzük:
A megszerzett egyenlőtlenséget a \ (T \) időszakot fejezzük ki, a probléma megoldását általános formában kapjuk meg:
Válasz: 160 perc.
Ha tetszett a feladatnak és megoldásának, akkor megoszthatja barátaival ezekkel a gombokkal.